Note: All comments and opinions expressed on "MATLAB for everyone" are mine alone and do not necessarily reflect those of my employers, past or present.

PID 제어란 무엇인가? 공학 초심자를 위한 직관적 이해 (Part 1)

해당 포스팅은 아래 영상의 설명을 기반으로 하였으며, Google Gemini의 도움을 받아 작성되었습니다.

이 포스팅에서 사용된 시뮬링크 모델들은 아래 링크에서 받으실 수 있습니다.

👉PID 101 Simulink Implementation

🚀 서론

공학 분야에서 PID 제어(Proportional-Integral-Derivative Control)는 가장 널리 사용되고 강력한 피드백 제어 기법 중 하나이다. 우리는 일상생활 속 수많은 시스템, 예를 들어 자동차의 크루즈 컨트롤, 보일러의 온도 유지, 드론의 자세 제어 등 다양한 분야에서 PID 제어의 원리가 활용된 경우가 많다.

이 글은 공학수학을 배우기 시작한 대학교 1학년 학생과 같이 제어 이론을 처음 접하는 독자를 위해, 복잡한 수학적 공식보다는 직관적인 이해에 초점을 맞추어 PID 제어의 기본 개념을 설명하는 데 목적이 있다. PID 제어의 세 가지 요소(비례, 적분, 미분)가 각각 어떤 역할을 하며, 왜 모두 필요한지에 대해 단계적으로 알아볼 것이다.

1. 제어 시스템의 기본 구조 및 오차 (Error)의 정의

모든 제어 시스템은 우리가 원하는 목표를 달성하기 위해 존재한다. 이를 이해하기 위해 몇 가지 용어를 정의한다.

플랜트 (Plant) 또는 시스템: 우리가 제어하고자 하는 대상이다. (예: 드론, 모터, 온도 조절기)
명령 (Command) 또는 목표값 (Set-point): 시스템이 도달해야 하는 원하는 값이다. (예: 고도 50m, 온도 25°C)
제어 변수(Controlled Variable) 혹은 출력 (Output): 플랜트의 현재 상태를 나타내는 측정값이다.
조작량 (Actuating Signal) 플랜트를 제어하기 위해 시스템에 가하는 신호이다. (예: 모터 회전 속도)

피드백 제어 (Feedback Control)의 핵심은 시스템의 출력을 다시 명령과 비교하여 그 차이를 계산하는 것이다. 이 차이를 오차(Error)라고 부른다.

\[\text{오차} = \text{명령} - \text{출력}\]

제어기의 목표는 이 오차를 0으로 수렴하게 만드는 조작량(입력)을 생성하는 것이다. [그림 1]은 이러한 피드백 제어 시스템의 기본적인 구조를 나타내는 블록 다이어그램이다.

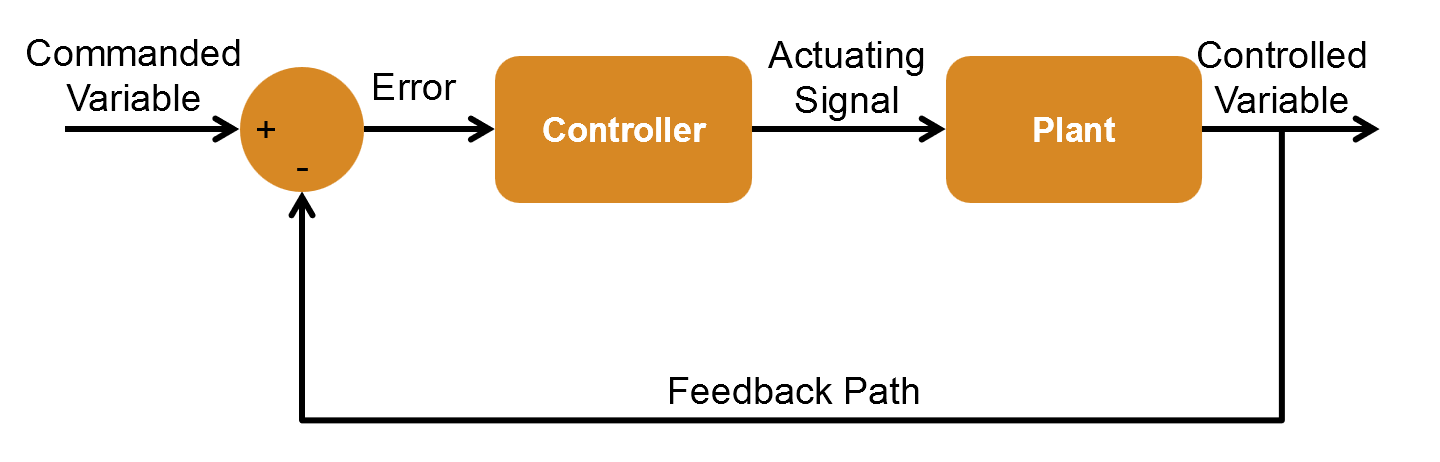
[그림 1] 피드백 제어 시스템의 기본 블록 다이어그램

2. 비례 제어 (Proportional Control, P 제어)의 원리

가장 단순한 형태의 제어는 비례 제어(P 제어)이다. P 제어는 현재의 오차 크기에 비례하는 조작량을 생성한다.

\[\text{조작량} = K_p \times \text{현재 오차}\]

여기서 $K_p$는 비례 이득(Proportional Gain)이며, 오차가 클수록 더 큰 힘을 가해 시스템을 빠르게 목표로 이동시키고, 오차가 작아질수록 힘을 줄여 부드럽게 멈추게 하는 역할을 한다. 마치 축구장 하프라인으로 걸어갈 때, 목표에서 멀수록 빠르게 걷고 가까워질수록 느리게 걷는 것과 유사하다.

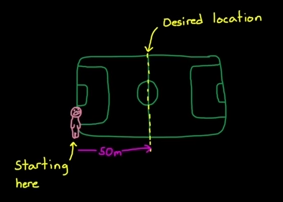
[그림 2] 비례 제어기(P Controller)의 비유: 축구장 왼쪽 끝에서 하프라인까지 걸어가게 만들기

맨 첫 번째 스텝에서는 희망 위치는 50 이지만 현재 위치는 0 이므로, 에러가 50에 이른다. 우리가 집중하고 있는 비례 제어 (Proportional Control)을 이용한다는 것은 그림 1의 Controller에 Gain 블록을 쓰는 것과 같다. 만약, Gain 블록의 값을 0.1이라고 한다면, $Error \times 0.1 = 50 \times 0.1 = 5$ 만큼 actuating signal로 입력을 줄 수 있게 된다. 이를 통해, 그림 2의 사람으로 표시된 “plant”는 5라는 입력만큼 걸어간다.

이제는 희망 위치가 50이고, 현재 위치는 5가 되므로, 에러가 45가 된다. Gain 값이 0.1이라면 actuating input은 4.5가 될 것이고, 사람(Plant)은 총 9.5만큼 걸어갔을 것이다. 이와 같이 Proportional Controller는 에러의 크기에 비례해 actuating signal 값을 주면서 plant의 출력값에 의해 발생하는 error가 0이 되도록 한다.

이를 시뮬링크에서 모델로 만들면 아래와 같다. 모델은 여기에서 받을 수 있는 “no1_proportional_controller.slx”라는 모델이다. 이 모델에서 Plant는 actuating input을 계속 누적해서 받으므로 integrator 블록을 이용했다.

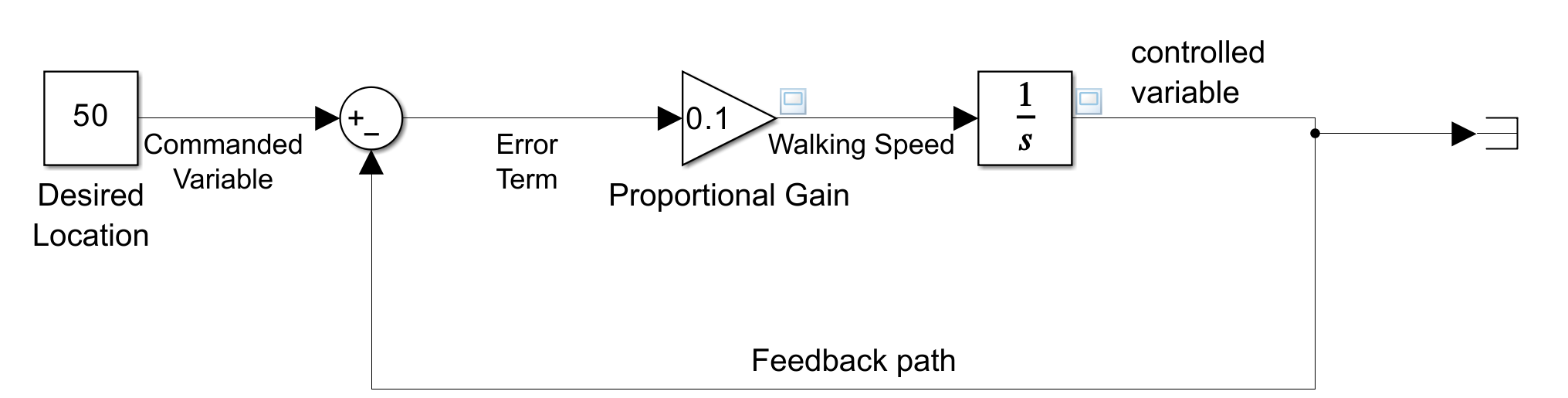
[그림 3] 비례 제어기(P Controller)를 포함한 제어 시스템의 블록 다이어그램과 P 제어만으로 구현된 Simulink 모델

시뮬레이션을 50초간 돌려보면 Walking Speed는 에러가 줄어듦에 따라 함께 줄어들고, Controlled Variable인 이동거리가 50에 점점 수렴하는 것을 알 수 있다.

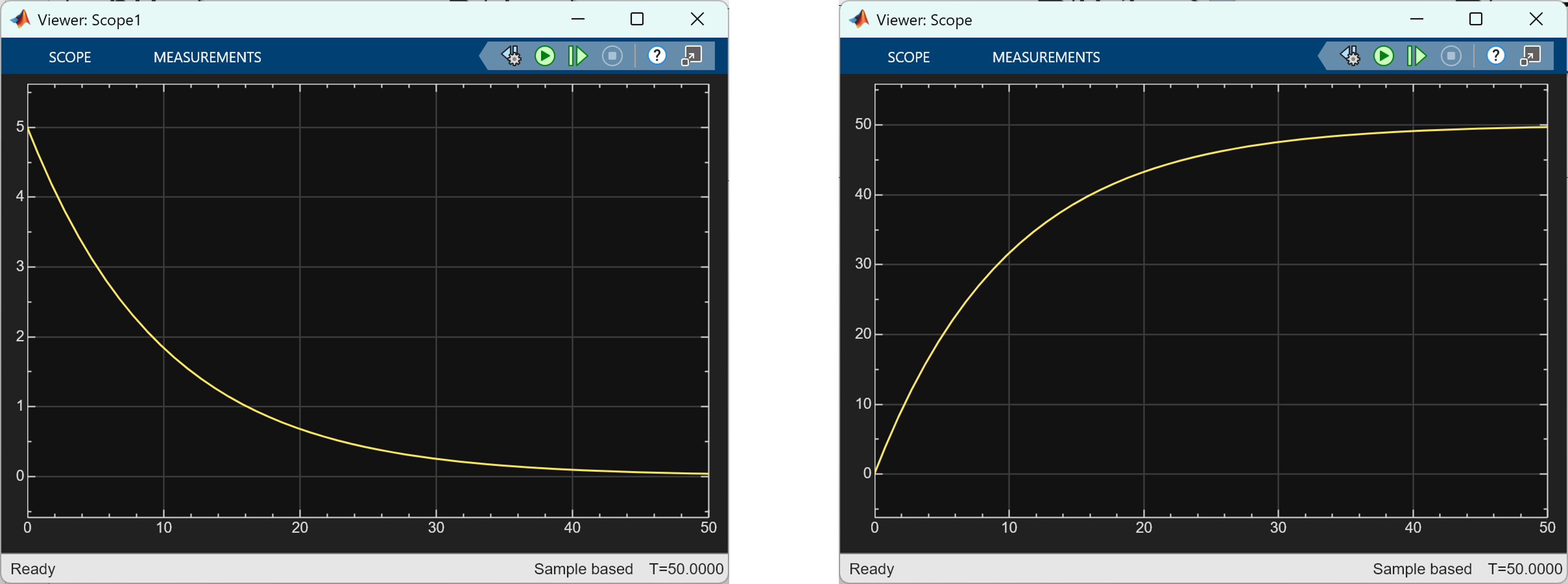
[그림 4] (왼쪽) 비례 제어기(P Controller)를 포함한 제어 시스템에서 Actuating Signal (Walking Speed)가 갈수록 줄어들고 있다. (오른쪽) Controlled Variable인 이동거리가 명령 변수 50에 가까워지는 것을 알 수 있다.

3. P 제어의 한계와 적분 제어 (Integral Control, I 제어)의 도입 (PI 제어)

P 제어는 간단하고 빠르게 반응하지만, 모든 상황에서 완벽하지는 않다. 특히, 중력과 같은 지속적인 외란이 존재하는 시스템(예: 드론의 고도 제어)에서는 정상 상태 오차(Steady-State Error)라는 문제가 발생한다.

드론을 50m 고도에 띄우려 할 때, P 제어는 오차가 0이 되는 순간 모터 출력을 멈춘다. 하지만 중력을 이기고 50m 고도를 유지하려면 모터가 계속 돌면서 특정 힘(예: 100RPM)을 내야 한다. P 제어는 오차가 0이 되면 출력을 0으로 만들기 때문에, 드론은 목표보다 낮은 고도(예: 30m)에서 모터 출력이 100RPM이 되어 중력과 균형을 이루고 멈추는 오차가 발생한다. 이것이 정상 상태 오차이다.

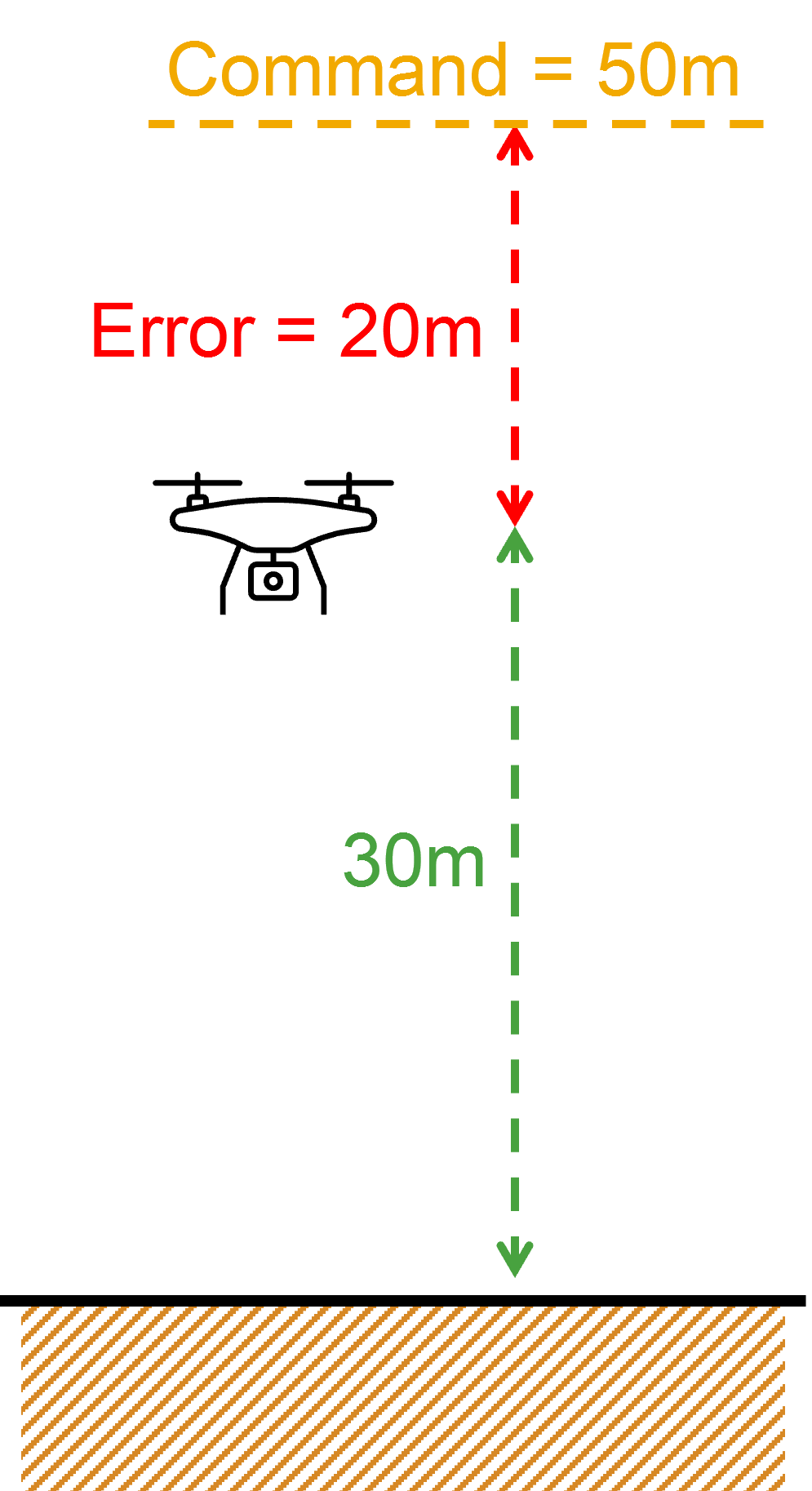
[그림 5] 드론이 계속 떠있기 위해서 어느정도의 추력(여기서는 100)이 필요하게 되며, 이에 의해 지속적으로 오차가 발생한다. 이 그림에서와 같이 P gain의 값이 5라면, 20 의 에러가 발생했을 때 지속적인 오차 (100)를 겨우 상쇄하면서 떠있을 수 있게 된다.

이 현상을 더 잘 이해하기 위해서 steady-state error가 도입되는 현상을 시뮬링크 모델에서 구현하자면 아래와 같다. 모델은 여기에서 받을 수 있는 “no2_proportional_controller_steady_state_error.slx”라는 모델이다.

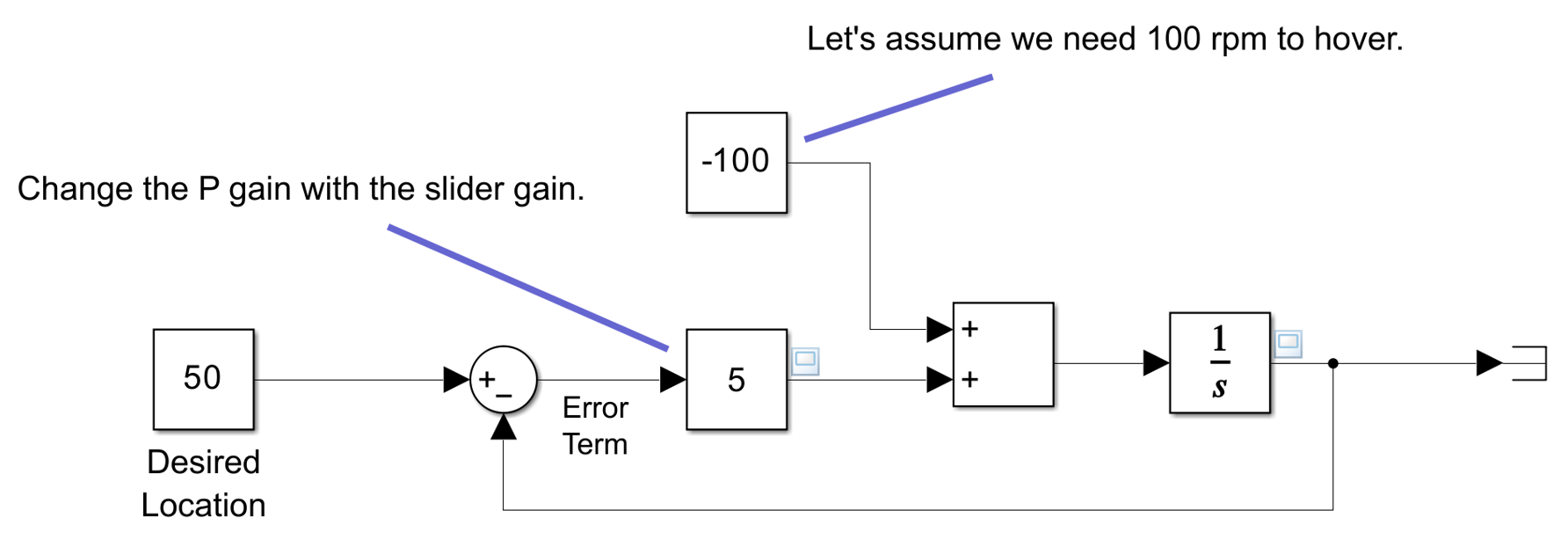
[그림 6] “-100”이라고 적힌 constant block이 steady-state error를 표현하고 있다. Error Term 및 P gain을 거쳐 나오는 actuating signal에 -100이라는 steady-state error 값이 지속적으로 추가되고 있다.

이 때, Scope 값을 찍어보면 고도는 30으로 계속 유지되는 것을 알 수 있다.

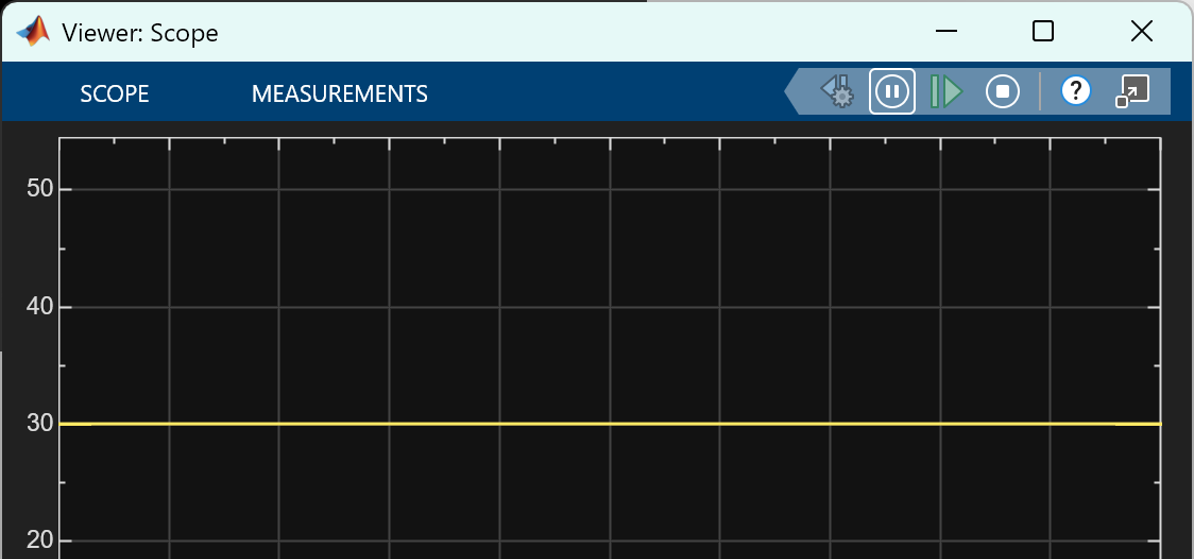
[그림 7] 그림 6의 steady-state error가 존재하는 상황에서의 고도 변화 시뮬레이션 결과

이 오차를 해결하기 위해 적분 제어(I 제어)가 도입된다. I 제어는 과거 오차를 모두 누적(적분)하여 조작량을 생성한다.

\[\text{조작량}_\text{I} = K_i \times \int (\text{과거 오차}) \, dt\]

시스템에 오차가 남아있는 한, 이 오차는 계속해서 누적되어 적분값이 증가한다. 이 누적된 값은 플랜트의 조작량을 점점 증가시켜, 결국 오차를 0으로 만들고 목표 지점에 도달하게 할 만큼 충분한 힘을 보상한다. 오차가 0이 된 후에도, 과거의 누적값은 그대로 유지되어 드론이 50m에서 중력을 이기고 호버링할 수 있도록 100RPM의 출력을 유지하게 하는 것이다.

P 제어와 I 제어를 합친 것을 PI 제어라고 한다. PI 제어는 정상 상태 오차를 제거하는 데 매우 효과적이다.

이 현상을 시뮬링크 모델에서 구현하자면 아래와 같다. 모델은 여기에서 받을 수 있는 “no3_PI_Controller.slx”라는 모델이다.

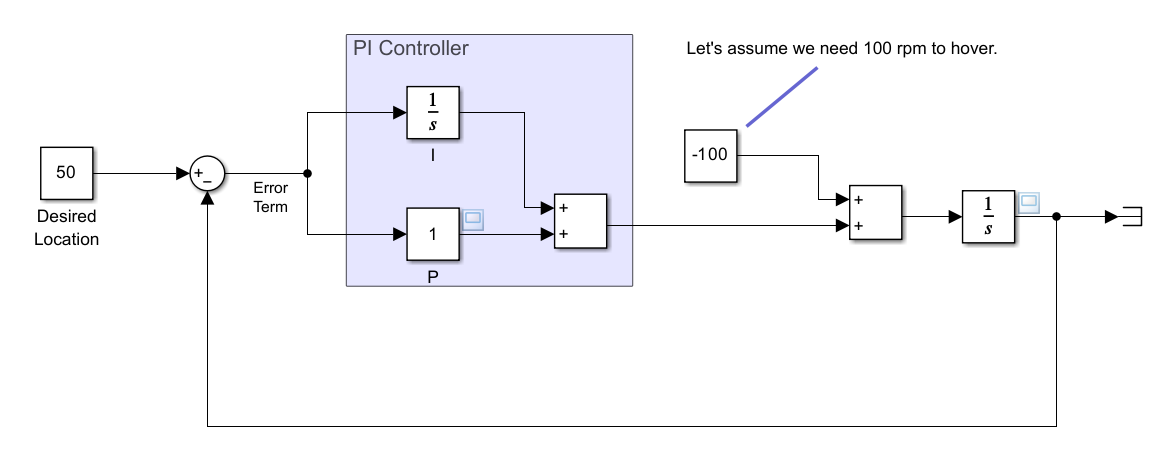
[그림 8] PI 제어기(PI Controller)를 포함한 제어 시스템의 블록 다이어그램과 PI 제어만으로 구현된 Simulink 모델

시뮬레이션 결과를 보면 PI 제어기를 이용하면 steady-state error를 효과적으로 상쇄할 수 있으며, 최종적으로 원하는 50m에 도달하게 되는 것을 알 수 있다.

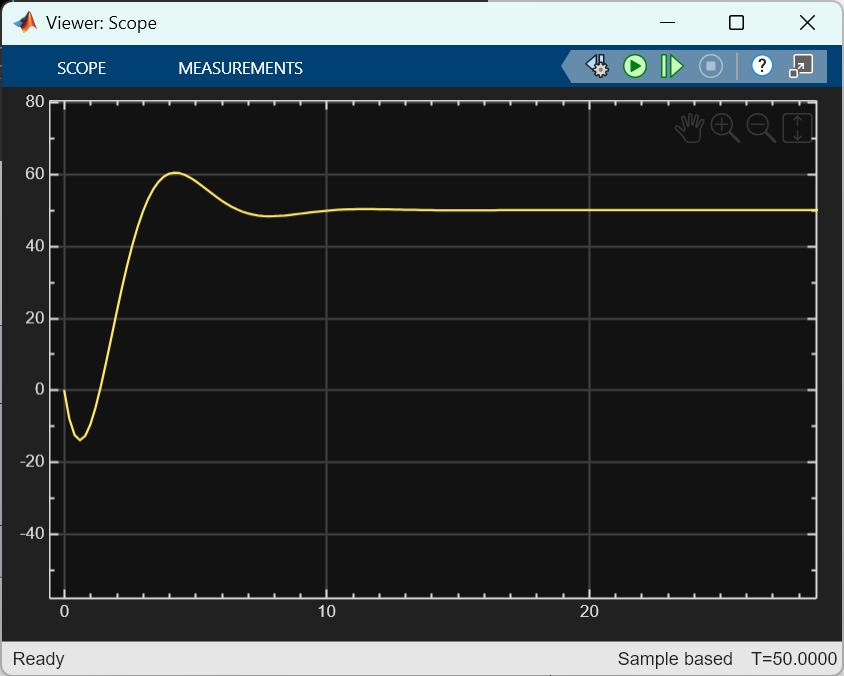
[그림 9] PI 제어기(PI Controller)를 포함한 제어 시스템의 시뮬레이션 결과

4. PI 제어의 한계와 미분 제어 (Derivative Control, D 제어)의 도입 (PID 제어 완성)

PI 제어는 정상 상태 오차를 제거하지만, 시스템의 응답 속도를 빠르게 하려다 보면 목표 지점을 지나쳤다가 다시 돌아오는 오버슈팅(Overshooting)과 진동 문제가 쉽게 발생한다. (이 현상을 그림 9에서 확인할 수 있다. 신호가 60까지 올라갔다가 다시 50으로 내려온다.) 이는 I 제어가 과거의 오차만을 보기 때문에 미래를 예측하지 못하기 때문이다.

오버슈팅을 방지하고 시스템의 안정성을 높이기 위해 미분 제어(D 제어)가 도입된다. D 제어는 오차의 변화율(Rate of Change), 즉 오차가 얼마나 빠르게 줄어들고 있는지를 보고 조작량을 생성한다.

\[\text{조작량}_\text{D} = K_d \times \frac{d}{dt} (\text{오차})\]

드론이 목표 고도에 빠르게 접근할 때(오차가 급격히 감소할 때), 오차의 변화율은 큰 음수 값을 가진다. D 제어는 이 음수 값에 비례하는 제어 신호를 발생시켜, 목표에 도달하기 직전에 미리 속도를 줄이는 역할을 한다. 이는 마치 자동차로 목적지에 접근할 때, 브레이크를 밟아 속도를 미리 감속하여 목표 지점을 정확하게 통과하는 것과 같다.

이로써 PID 제어(Proportional-Integral-Derivative Control)가 완성된다. PID 제어는 현재(P), 과거(I), 미래(D)의 오차 정보를 모두 사용하여 시스템을 가장 빠르고 안정적이며 정확하게 제어할 수 있는 보편적인 제어 방식이 되는 것이다. 모델은 여기에서 받을 수 있는 “no4_PID_Controller.slx”라는 모델이다.

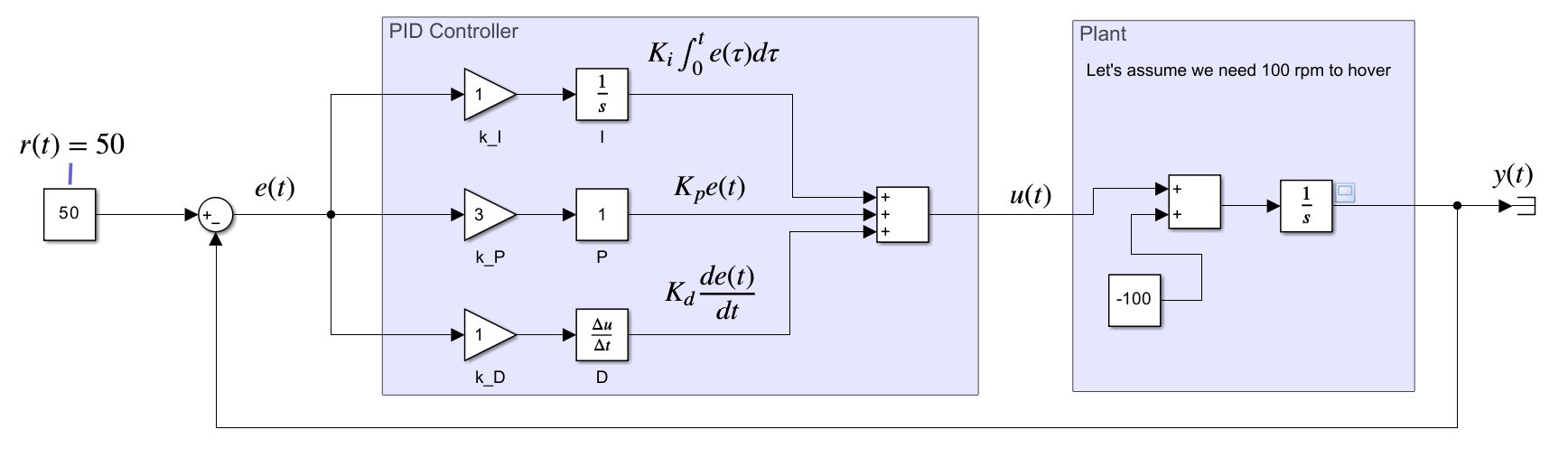
[그림 10] 최종적인 PID 제어기(PID Controller)를 포함한 제어 시스템의 블록 다이어그램과 PID 제어로 완성된 Simulink 모델

시뮬레이션 결과에서도 오버슈팅이 사라지고, 부드럽게 신호가 원하는 고도인 50 으로 값이 바뀌는 것을 알 수 있다.

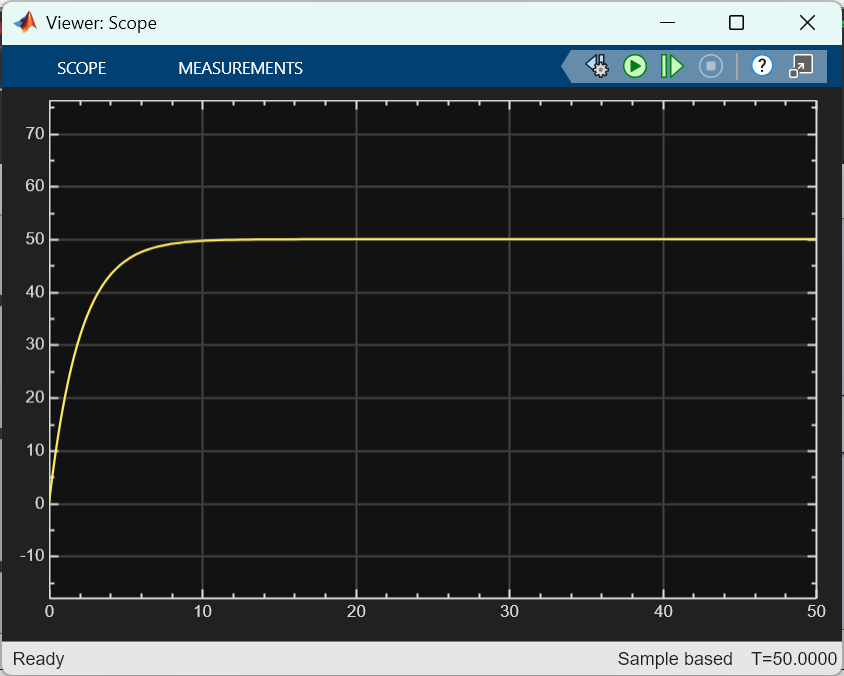
[그림 11] 최종적인 PID 제어기(PID Controller)를 포함한 모델의 시뮬레이션 결과. PI 제어기에서 발생한 오버슈팅이 사라지는 것을 볼 수 있다.

5. 결론 및 다음 단계

PID 제어는 세 가지 요소, 즉 비례(P)는 현재 오차에 반응하여 응답 속도를 결정하고, 적분(I)은 과거 오차를 누적하여 정상 상태 오차를 제거하며, 미분(D)은 오차의 변화율을 감지하여 오버슈팅을 방지하고 안정성을 확보한다. 이 세 가지 요소의 게인값 ($K_p, K_i, K_d$)을 조정(튜닝)하는 과정을 통해 원하는 성능을 얻을 수 있다.

PID 제어는 공학에서 가장 기본적인 제어기로서, 그 원리를 직관적으로 이해하는 것은 모든 제어 이론 학습의 출발점이다. 다음 글에서는 PID 제어기를 실제로 Simulink로 구현해보고, 각 게인값 변화에 따른 시스템의 응답을 관찰하는 튜닝(Tuning) 과정에 대해 심층적으로 다루어 볼 것이다.

PID 제어기란 무엇인가