Cleve Moler & Jakc Little이 쓴 A history of MATLAB(2020)을 번역했습니다.

Note: All comments and opinions expressed on "MATLAB for everyone" are mine alone and do not necessarily reflect those of my employers, past or present.

Important: 원문의 첫 페이지에서 다음과 같이 확인할 수 있는 문구를 바탕으로 본 페이지의 번역물을 디지털 방식으로 작성하여 공개하는 것임을 알려드리며 본 페이지에서는 어떠한 상업적 이익도 발생하지 않는다는 것을 알려드립니다.

Permission to make digital or hard copies of part or all of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. Copyrights for third-party components of this work must be honored. For all other uses, contact the owner/author(s).

본 게시글의 원문은 Cleve Moler & Jack Little의 A history of MATLAB(2020) 이며 공식 citation은 아래와 같습니다.

Cleve Moler and Jack Litle. 2020. A History of MATLAB. Proc. ACM Program. Lang. 4, HOPL, Article 81 (June 2020), 67 pages. https://doi.org/10.1145/3386331

본 포스팅에는 원문의 부록이나 참고 문헌은 포함하지 않았습니다. 따라서, 부록 혹은 참고 문헌에 대한 정보는 원문에서 확인하여 주십시오.

Abstract

첫 번째 MATLAB® (이름은 “Matrix Laboratory”의 줄임말)은 프로그래밍 언어가 아니었습니다. 1970년대 후반에 Fortran으로 작성되었으며, 약 열두 개의 서브루틴으로 구성된 LINPACK 및 EISPACK 행렬 소프트웨어 라이브러리를 기반으로 한 간단한 대화형 행렬 계산기였습니다. 예약어와 내장 함수는 총 71개뿐이었습니다. 이를 확장하려면 Fortran 소스 코드를 수정하고 다시 컴파일해야 했습니다.

프로그래밍 언어는 1984년 MATLAB이 상용 제품이 된 때 등장했습니다. 이 계산기는 C로 다시 구현되었으며 사용자 함수, 툴박스, 그래픽을 추가하여 크게 향상되었습니다. 초기에는 IBM PC 및 클론에서 사용할 수 있었고, 이후 Unix 워크스테이션 및 Apple Macintosh용 버전이 곧 출시되었습니다. 이 계산기의 행렬 함수에 추가로 1984년 MATLAB은 빠른 푸리에 변환(FFT)을 포함하고 있었습니다. 제어 시스템 툴박스™는 1985년에 등장하고, 신호 처리 툴박스™는 1987년에 등장했습니다. 또한 1987년에는 일반 미분 방정식의 수치 해법을 위한 내장 지원이 추가되었습니다.

첫 번째 중요한 새 데이터 구조인 희박 행렬은 1992년에 소개되었습니다. 이미지 처리 툴박스™와 심볼릭 수학 툴박스™가 모두 1993년에 소개되었습니다. 1990년대 후반에는 단정밀 부동 소수점, 다양한 정수 및 논리형 타입, 셀 배열, 구조체 및 객체와 같은 여러 새로운 데이터 유형과 데이터 구조가 도입되었습니다.

최근 몇 년간 MATLAB 컴퓨팅 환경 개선이 지배적이었습니다. 데스크탑에 대한 확장, 객체 및 그래픽 시스템에 대한 주요 개선, 병렬 컴퓨팅과 GPU 지원, 그리고 “Live Editor”가 포함되어 있으며, 이는 프로그램, 설명 텍스트, 출력 및 그래픽을 단일 대화형 서식 문서로 결합합니다. 오늘날은 MATLAB 언어로 프로그래밍된 많은 툴박스가 있으며, 전문적인 기술 분야에서 확장된 기능을 제공하고 있습니다.

프롤로그

1966년 대학원 졸업 후 첫 직장에서 Cleve Moler는 수학 조교수로 재직했습니다. 그는 미적분학, 수치해석학, 그리고 선형대수학을 가르쳤습니다. 선형대수학 수업에서는 추상적인 벡터 공간에서 선형 변환에 관한 정리들의 증명을 강조하는 전통적인 강의 계획을 따랐습니다. 컴퓨터나 행렬의 응용에는 시간을 할애하지 않았습니다. 이후 그는 절대로 전통적인 강의 계획을 다시 따르지 않기로 다짐했습니다. 그는 특잇값 분해와 같은 행렬 인수분해를 사용하고, 주성분 분석과 같은 응용을 강조하고자 했습니다. 또한 학생들이 컴퓨터와 현대 소프트웨어를 사용하도록 원했습니다. 전통적인 선형대수학을 대체할 새로운 과목으로 “행렬 분석(matrix analysis)”이라는 코스를 개설하고자 했습니다.

그림 1. MATLAB 개발 중 주요 사건들

1. MATLAB®의 창조

MATLAB의 원래 목표는 원래 발행된 설계 설명서 소개에서 잘 표현되어 있습니다 [Moler 1980; Moler 1982도 참조]:

MATLAB은 행렬을 사용하는 계산에 편리한 "실험실"로서 작동하는 대화형 컴퓨터 프로그램입니다. 이는 LINPACK 및 EISPACK 프로젝트 [Dongarra 등 1979; Garbow 등 1977; Smith 등 1974]에서 개발된 행렬 소프트웨어에 쉽게 접근할 수 있습니다. 기능은 동시 선형 방정식의 해결과 행렬의 역행렬 구하기부터 대칭 및 비대칭 고유값 문제에서 특이값 분해와 같은 꽤 복잡한 행렬 도구에 이르기까지 다양합니다.

MATLAB의 주요 사용 사례 중 하나는 수업에 활용하는 것입니다. 이는 응용 선형 대수학의 입문 강좌에서부터 수치해석, 행렬 이론, 통계 및 기타 학문에 행렬을 적용하는 고급 과정에 유용하게 사용될 것으로 예상됩니다. 학교 외의 환경에서는 MATLAB이 행렬을 사용하는 작은 문제의 빠른 해결을 위한 "책상용 계산기"로 활용될 수 있습니다.

이 프로그램은 Fortran으로 작성되었으며, 대화형 실행을 허용하는 모든 운영 체제에 쉽게 설치될 수 있도록 설계되었습니다. 필요한 자원은 상당히 절제되었습니다. LINPACK과 EISPACK 하위 루틴이 사용된 포함되어 약 6,000 줄의 Fortran 소스 코드가 있습니다. 오버레이의 적절한 사용으로 32K 바이트의 메모리만 있는 미니컴퓨터에서 시스템을 실행할 수 있습니다.

MATLAB에서 처리할 수 있는 행렬의 크기는 특정 기기에서 시스템을 컴파일할 때 설정된 저장소 양에 따라 달라집니다. 일반적으로 행렬 요소에 대해 4,000 워드의 할당이 충분히 만족스럽습니다. 이는 예를 들어 여러 개의 20x20 행렬을 저장하는 데 충분한 공간을 제공합니다. 가상 메모리 시스템의 한 구현은 50,000개의 요소를 제공합니다. 사용되는 대부분의 알고리즘은 메모리에 순차적으로 액세스하기 때문에 할당된 대용량 저장소는 어려움이 없습니다.

어떤 면에서 MATLAB은 SPEAKEASY [NA Cohen 1973]와 APL과 유사합니다. 모두 대화형 터미널 언어로서 보통 한 줄 명령이나 문장을 받아들이고 즉시 처리하며 결과를 출력합니다. 모두 배열 또는 행렬을 주요 데이터 유형으로 갖고 있습니다. 그러나 MATLAB에서는 행렬이 유일한 데이터 유형입니다 (스칼라, 벡터 및 텍스트는 특수한 경우입니다). 기반 시스템은 휴대성이 있으며 더 적은 자원을 필요로 하며 지원 서브루틴은 더 강력하며 일부 경우에는 더 좋은 수치적 특성을 가지고 있습니다.

LINPACK과 EISPACK은 행렬 계산을 위한 소프트웨어 분야의 최첨단 기술을 대표합니다. EISPACK은 주로 Wilkinson과 Reinsch 및 그 동료들이 발행한 Algol 절차에 기반한 다양한 행렬 고유값 계산을 위한 70개 이상의 Fortran 하위 루틴 패키지입니다. LINPACK은 동시 선형 방정식과 관련 행렬 문제를 해결하고 분석하기 위한 40개의 Fortran 하위 루틴 패키지(각각 4개의 데이터 유형에 해당)입니다. MATLAB은 실행 시간 효율성이나 저장 공간 절약에 주로 관심이 없으므로, LINPACK과 EISPACK 하위 루틴이 이용하는 대부분의 특수한 행렬 특성을 무시합니다. 따라서 실제로 사용되는 LINPACK 하위 루틴은 8개이며, EISPACK은 5개만이 관련됩니다.

MATLAB이 APL과 SPEAKEASY와 다른 가장 중요한 점은 휴대성입니다. APL은 특정 문자 집합을 위해 특별한 I/O 장비를 필요로 하고, SPEAKEASY는 IBM 타임셰어링 시스템에서만 실행됩니다. Moler는 학생들에게 널리 사용될 수 있도록 다양한 컴퓨터와 운영 체제에서 쉽게 컴파일하고 실행될 수 있는 도구를 만들고자 했습니다. MATLAB의 다른 중요한 특징으로는 고품질의 수치 알고리즘 사용, 사용자 터미널에서 대화형 플롯 생성 기능(일부 SPEAKEASY 구현은 고품질 플롯을 지원하지만 상당히 느린 CalComp 플로터를 사용하여 “대화형”이라는 일반적인 의미에서는 아닙니다) 및 역슬래시 연산자가 있습니다(2.1절 참조).

1.1 수학적 기원

Moler는 그의 전문 분야인 선형 방정식 시스템에 큰 관심을 가지고 있으며, 이러한 시스템은 종종 행렬 형태로 표현됩니다. 1965년에 스탠퍼드 대학에서 박사 학위를 받은 이후, Moler는 자신의 박사 학위 지도 교수이자 스탠퍼드 대학 컴퓨터 과학 부문 설립자인 George Forsythe와 함께 선형 방정식 시스템을 해결하기 위한 개선된 계산 방법에 대해 계속해서 연구하였으며, 그들은 함께 책을 저술하기도 했습니다[Forsythe and Moler 1967; Moler 1967, Moler 1969, na Moler 2013b도 참조].

MATLAB의 첫 번째 버전에 대한 수학적 및 계산적 기초는 J. H. Wilkinson과 그의 동료들에 의해 1965년부터 1970년까지 Numerische Mathematik 저널에 발행된 일련의 논문으로 시작합니다. 이 논문들은 Algol 60로 구현된 행렬 선형 방정식 및 고유값 문제를 해결하기 위한 알고리즘을 제시했습니다. 이들은 수치적 안정성에 관한 결과, 구현의 세부 사항 및 새로운 방법에 대한 연구 논문들로서, 가능한 한 직교 변환을 사용하는 중요성이 Wilkinson과 다른 저자들에 의해 강조되었습니다. Part I에서는 40개의 Algol 절차로 선형 방정식 문제를 다루고, Part II에서는 43개의 절차로 고유값 문제를 다루고 있습니다. 개별 절차 목록은 [NA Moler 2017]에서 제공됩니다.

1.2 EISPACK

1970년에 Handbook이 출판되기 전에, Argonne National Laboratory의 한 그룹이 미국 국립과학재단(NSF)에게 “고품질의 수학적 소프트웨어를 생산, 테스트, 보급하는 데 필요한 방법론, 비용 및 자원을 탐구하고, 특정 문제 영역의 수학적 소프트웨어 패키지를 테스트, 인증, 보급, 지원하는 데 필요한 것들을 검증하는” 제안서를 제출했습니다.

15년 동안 매년 여름에 Wilkinson은 미시간 대학교에서 단기 강좌를 강의하고, 이후에는 Argonne National Laboratory를 방문했습니다(그림 2 참조). 이 프로젝트는 Handbook의 Part II에 있는 고유값 문제를 위한 Algol 절차들을 Fortran으로 번역하고, 테스트와 이식성에 많은 노력을 기울여 EISPACK(Matrix Eigensystem Package)을 개발했습니다.

1971년, 이러한 컬렉션의 첫 번째 릴리스는 약 2십여개의 대학교와 국립 연구소로 발송되었으며, 프로젝트에 관심을 보인 개인들이 소프트웨어를 테스트하기로 동의한 곳에 보내졌습니다[Smith 등 1974]. 1976년에는 두 번째 릴리스가 준비되어 공개 배포가 이루어졌습니다[Garbow 등 1977]. Handbook의 Part II에서 유도된 하위 루틴 외에도, 두 번째 릴리스에는 Part I에서의 SVD 알고리즘과 두 개의 행렬을 포함하는 일반화된 고유값 문제를 위한 새로운 QZ 알고리즘이 포함되었습니다.

EISPACK에 대한 자세한 내용은 [NA Moler 2018a]를 참조하십시오.

1.3 LINPACK

1975년, EISPACK이 마무리 단계에 접어들 때, Jack Dongarra, Pete Stewart, Jim Bunch, 그리고 Cleve Moler (그림 3 참조)은 또 다른 수학적 소프트웨어 개발 방법을 조사하기 위한 연구 프로젝트를 NSF에 제안했습니다. 부산물은 “선형 방정식 패키지”로 명명된 소프트웨어였습니다[Dongarra 등 1979]. 이 프로젝트 또한 Argonne에서 집중적으로 진행되었습니다. 대학교에서 참여한 세 명의 참가자는 학년중 자신들의 학교에서 작업하였고, 네 명 모두 여름에 Argonne에서 함께 모였습니다.

그림 2. J. H. Wilkinson이 1970년대 초 Argonne에서 청중에게 행렬 알고리즘을 설명하는 모습 (출처: Argonne National Laboratory)

LINPACK은 Fortran에서 개발된 것으로, Algol에서의 번역 과정은 없었습니다. 이 패키지에는 REAL, DOUBLE, COMPLEX 및 COMPLEX*16의 네 가지 정밀도로 각각 44개의 하위 루틴이 포함되어 있었습니다. 당시 Fortran은 구조화되지 않고 읽기 어려운 “스파게티” 코드로 유명했습니다. 그러나 LINPACK 개발자들은 체계적인 프로그래밍 스타일을 채택하고, 사람들과 기계 모두가 코드를 읽을 수 있도록 노력했습니다. 루프와 if-then-else 구문의 범위는 들여쓰기를 통해 명확하게 표시되었습니다. Go-to 및 문장 번호는 블록을 종료하고 빈 루프를 처리하는데에만 사용되었습니다.

모든 내부 루프는 Caltech의 Jet Propulsion Laboratory에서 Chuck Lawson과 동료들이 동시에 개발한 기본 선형 대수 서브프로그램(BLAS)을 호출하여 수행되었습니다 [Lawson 등 1979]. 최적화되지 않은 Fortran 컴파일러를 갖추지 않은 시스템에서는 BLAS를 기계어로 효율적으로 구현할 수 있었습니다. 벡터 기계인 CRAY-1과 같은 시스템에서는 루프가 단일 벡터 명령으로 처리되었습니다. 가장 중요한 두 가지 서브프로그램은 두 벡터의 내적인 DDOT과 벡터와 스칼라의 합인 DAXPY입니다. 모든 알고리즘은 Fortran 저장 방식에 맞게 열 지향적으로 설계되어 메모리 접근의 국소성을 제공했습니다. [Moler 1972]

LINPACK과 EISPACK 프로젝트는 어느 정도로는 실패했습니다. 연구자들은 “고품질의 수학적 소프트웨어를 생산, 테스트, 보급하는 데 필요한 방법론, 비용 및 자원을 탐구하고, 특정 문제 영역의 수학적 소프트웨어 패키지를 테스트, 인증, 보급, 지원하는 데 필요한 것들을 검증하는” 제안서를 NSF에 제출했지만, 이러한 목표를 다루는 보고서나 논문은 쓰지 않았습니다. 그들은 단지 소프트웨어를 개발한 것 뿐이었습니다. [Boyle 등 1972]

LINPACK 내용에 대한 요약은 [na Moler 2018b]를 참조하십시오.

오늘날, LINPACK은 행렬 소프트웨어 라이브러리보다는 벤치마크로 더 잘 알려져 있습니다. LINPACK 벤치마크에 대해서는 [na Moler 2013e]를 참조하십시오.

그림 3. LINPACK의 저자들: Jack Dongarra, Cleve Moler, Pete Stewart, 그리고 Jim Bunch (1978년). (출처: Cleve Moler)

1.4 클래식 MATLAB

1970년대와 초기 1980년대에 Cleve Moler는 LINPACK과 EISPACK 프로젝트에 참여하면서 뉴 멕시코 대학교 앨버커키 캠퍼스에서 수학 교수로 재직하였습니다. 그는 선형 대수학과 수치 해석학 과목을 가르치고 있었습니다. 그는 학생들이 Fortran 프로그램을 작성하지 않고도 LINPACK과 EISPACK 함수에 쉽게 접근할 수 있기를 원했습니다. “쉬운 접근”이라는 것은 일반적으로 대학교 중앙 메인프레임 컴퓨터에서 필요한 원격 배치 처리와 반복적인 편집-컴파일-링크-로드-실행 프로세스를 피하는 것을 의미합니다. 이것은 프로그램이 가능한 한 빠르게 작동하는 대화형 인터프리터여야 한다는 것을 의미했습니다. 이러한 대화형 시스템은 시분할 시스템으로 이용 가능해지고 있었습니다.

그래서 Moler는 Niklaus Wirth의 책 “알고리즘 + 데이터 구조 = 프로그램” [Wirth 1976]을 공부하여 프로그래밍 언어를 파싱하는 방법을 배웠습니다. Wirth는 이 예제 언어를 PL/0라고 부르며, 이는 Wirth의 Pascal의 교육용 하위 집합 언어이며, 또한 Algol에 대한 응답으로 개발되었습니다. Wirth의 말을 인용하면 “자료형의 영역에서 PL/0는 단순함과 타협없는 요구를 따릅니다. 정수만이 그 유일한 자료형입니다.”

Wirth의 접근 방식을 따라, Moler는 Fortran에서 PL/0의 변형으로 행렬(matrix)만을 데이터 유형으로 갖는 최초의 MATLAB을 작성했습니다. 이 프로젝트는 그저 그가 배울 새로운 프로그래밍 방법이자 학생들에게 제공할 무언가였습니다. 현재 MathWorks가 운영되고 있는 상업적인 기업은 몇 년 후에 탄생한 것이며, 이 당시에는 어떠한 공식적인 외부 지원이나 사업 계획도 없었습니다.

그림 4. 1981년 5월 12일 버전의 MATLAB 시작 화면

이 최초의 MATLAB은 프로그래밍 언어가 아니었습니다. 그저 간단한 대화형 행렬 계산기일 뿐이었습니다. 사용자 정의 함수, 툴박스, 그래픽은 없었고, 또한 ODE(Ordinary Differential Equations, 상미분 방정식)이나 FFT(Fast Fourier Transform, 고속 푸리에 변환)도 없었습니다. 그림 4에 나와있는 기동화면 스냅샷에는 모든 함수와 예약어가 나열되어 있습니다. 총 71개의 항목이 있었습니다. 새로운 함수를 추가하고 싶다면 Moler에게 소스 코드를 요청하여 Fortran 서브루틴을 작성하고, 새로운 이름을 파싱 테이블에 추가한 후 MATLAB을 다시 컴파일하면 됩니다.

이 “클래식 MATLAB”의 전체 1981 사용자 가이드는 [na Moler 1981]에서 확인할 수 있습니다.

2. 클래식 MATLAB의 주요 기능

클래식 MATLAB은 단순한 행렬 계산기일 수 있었지만, 여전히 오늘날에도 사용되는 몇 가지 명령어와 연산자를 포함하고 있었습니다. 특히, 역슬래시 연산자 ‘'(일련의 선형 방정식을 해결하는 데 사용)와 콜론 연산자 ‘:’(정수나 실수로 이루어진 벡터를 계산하는 데 사용)는 수치 선형 대수를 넘어서 MATLAB이 확장되면서 많은 다른 분야에서 유용하게 쓰이게 되었습니다.

2.1 역슬래시 연산자

행렬 계산에서 가장 중요한 작업은 동시 선형 방정식의 해를 구하는 것입니다:

\[Ax = b\]

여기서 $A$는 정방 행렬(square matrix), $b$는 열 벡터(column vector)이며, 원하는 해 $x$도 다른 열 벡터(column vector)입니다. 계산 효율성과 정확성을 고려하지 않는다면, 전통적으로 해를 구하는 표기법은 행렬 역행렬, $A^{-1}$을 사용하는 것입니다:

\[x=A^{-1}b\]

하지만, 제한된 정밀도 산술에서 발생하는 반올림 오차로 인해 행렬 역행렬을 계산하지 않고도 직접적으로 시스템을 효율적으로 그리고 정확하게 해결하는 것이 더 좋습니다. (스칼라 경우를 생각해 보면 $7x = 21$을 해결하는 것은 $7$로 양변을 나누는 것으로 얻어지며, $7^{-1} = .142857 … $ 을 사용하여 양변에 곱하는 것이 아닙니다.) 따라서 수학적으로 금기시된 행렬 좌측 나눗셈 개념이 도입되며, 역슬래시 문자가 가우스 소거 과정을 통해 얻은 해를 나타냅니다.

x = A\b

비슷한 방정식을 나타내는 행 벡터에 대한 연산은 행렬 우측 나눗셈을 사용하여 얻을 수 있으며, 이는 (당연하게도) MATLAB에서는 슬래시를 사용하여 표현됩니다:

x = b/A

그 당시에 사용되고 있던 모든 문자 집합은 Bob Bemer의 노력 덕분에 슬래시와 역슬래시 문자를 모두 가지고 있었습니다 [na Bemer 2000; na Moler 2013a].

APL과 SPEAKEASY는 모두 행렬 우측 나눗셈을 위한 연산자를 갖고 있었습니다. 이 연산자의 구문은 일반적인 부동 소수점 수의 나눗셈과 유사하게, 나눗셈 대상을 왼쪽에, 나누는 수를 오른쪽에 두는 것입니다. 그러나 행렬 형태로 표현된 선형 방정식을 다루는 수학자들은 많은 수십 년 동안 $Ax=b$ 형태의 열 벡터와 방정식을 사용하는 것을 선호해왔기 때문에 일반적으로 행렬 좌측 나눗셈 '\'을 사용하는 것이 '/'보다 훨씬 편리합니다. (행렬 우측 나눗셈을 제공하는 모든 언어에서는 선형 방정식 $Ax = b$를 해결하는 데에도 사용할 수 있지만, 결과를 얻기 위해서는 인수들과 결과를 전부 전치(transpose)해야 합니다. MATLAB에서는 이를 x = (b'/A')'와 같이 쓸 수 있지만, 이렇게 되면 불필요하게 불편해집니다.)

오늘날, 행렬 할당 문장

x = A\b;

가 MATLAB을 대표하는 문장으로 자리잡았습니다. 이 문장만 적혀있는 티셔츠는 아주 인기가 있으며, MathWorks는 학회에서 이런 티셔츠를 무료로 나누어주기도 합니다. (그림 5를 참조하세요.)

그림 5. 이 인기 있는 티셔츠에는 상징적인 MATLAB 역슬래시 연산이 특징으로 나타나 있습니다. (출처: Patsy Moler.)

2.2 콜론 연산자

콜론 연산자는 MATLAB에서 중요한 역할을 합니다:

$\Rightarrow$ a:d:b는 행 벡터 $\begin{bmatrix}a, a+d, a + 2d, \cdots, a+nd\end{bmatrix}$ 을 나타내며, 여기서 $n=\text{floor}((b-a/d))$입니다.

만약 d = 1이라면, 생략할 수 있습니다:

$\Rightarrow$ a:b는 행 벡터$\begin{bmatrix}a, a+1, a + 2, \cdots, a+n\end{bmatrix}$을 나타내며, 여기서 $n=\text{floor}(b-a)$입니다.

다음은 몇 가지 예시입니다:

1:10은 1부터 10까지의 정수로 이루어진 행 벡터입니다.
0:0.1:10은 길이가 101인 행 벡터 [0, 0.1, 0.2, . . . , 9.8, 9.9, 10.0]입니다.
‘A’:’Z’는 26개의 대문자 알파벳으로 이루어진 문자열입니다.
A(i:m,j:n)은 행렬 A의 하위 행렬(submatrix)입니다.
아래의 스크립트는 <statements>들을 n 번 실행합니다.

for k = 1:n
    <statements>
end

나중에 1:end의 약어로서 콜론 자체가 추가되었습니다.

A(:,3)은 행렬 A의 세 번째 열을 나타냅니다.
A(:)은 행렬 A의 모든 요소를 한 줄로 늘어놓은 긴 열 벡터입니다.

2.3 why 명령어

Classic MATLAB에 이미 what, while, who가 있었기 때문에, Moler는 why를 추가했습니다. why는 단순히 고정된 목록에서 무작위 응답을 반환합니다. 이 기능은 매우 인기가 있었습니다. why의 예시:

WHY NOT?

그리고

INSUFFICIENT DATA TO ANSWER.

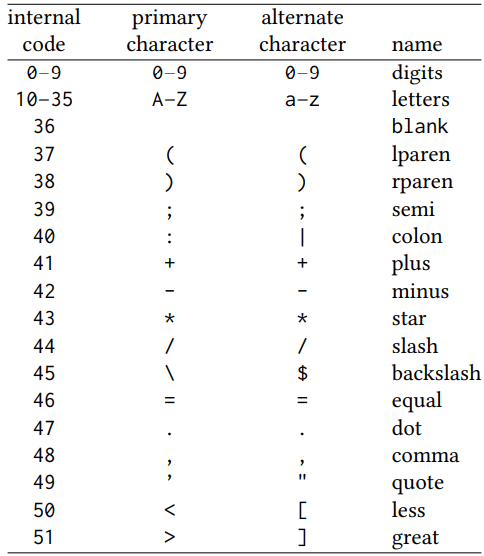
그림 6. Classic MATLAB에서 내부적으로 사용되는 문자 코드 표

2.4 Portable Character Set

Portable Character Set를 사용하는 Classic MATLAB은 Pascal과 Fortran 77에서 사용하는 것과 유사한 텍스트 문자열에 대해 상당히 관습적인 표기법을 가졌습니다. 그러나 Classic MATLAB은 별도의 “문자열” 데이터 유형은 없었습니다.

'abcxyz'
    ANS =
    10 11 12 33 34 35

텍스트 문자열은 단지 $1\times n$ 행 벡터 (즉, 1-바이-𝑛 행렬)을 나타내는 방법 중 하나였으며, 각 문자는 MATLAB 내부적으로 사용되는 52개의 문자 코드 중 하나로 인코딩되었습니다.

' < > ( ) = . , ; \ / '
ANS =
    COLUMNS 1 THRU 12
    36 50 36 51 36 37 36 38 36 48 36 37
    COLUMNS 13 THRU 21
    36 48 36 39 36 45 36 44 36

disp 함수는 이러한 행렬로 인코딩된 문자를 터미널 상에 출력하는 데 사용할 수 있었습니다.

MATLAB은 이 문자 세트를 두 개의 열을 가진 테이블로 유지 관리했고 (그림 6 참조), 사용자에 의해 수정할 수 있었습니다. 각 열에는 52개의 항목이 있으며, 항목 𝑘은 MATLAB 내부 코드 𝑘에 해당하는 기계 특정 (또는 운영 체제 특정) 문자 코드였습니다. 이 테이블은 키보드 문자와 MATLAB 내부 코드 사이의 변환에 사용되었습니다.

입력 시에는 두 개의 기계 문자가 동일한 MATLAB 내부 코드로 매핑될 수 있었습니다. 이는 소문자를 대문자로 처리하도록 허용했으며, 또한 꺽쇠 대신 괄호를 사용할 수 있도록 허용했습니다. 또한, 함수 char는 정수 𝑘를 인수로 사용하고 키보드에서 문자 𝑐(한 번의 키 누름)를 직접 읽어들여 𝑘 ≥ 0이면 첫 번째 열의 항목 𝑘에, 𝑘 < 0이면 두 번째 열의 항목 −𝑘에 저장했습니다. 이렇게 함으로써 사용자가 특이한 키보드를 가진 시스템에서 MATLAB을 실행하는 경우 키보드에 맞게 테이블을 사용자 정의할 수 있었습니다. 이것이 MATLAB의 이식성(portability)의 중요한 측면입니다.

출력 시에는 간단한 색인을 사용하여 내부 코드를 기계 문자로 변환했습니다. 대부분의 경우 첫 번째 열이 사용되었지만 (예를 들어, 소문자로 입력한 변수 이름이 대문자로 출력되는 이유입니다), 때로는 두 번째 열이 사용되었습니다 (예를 들어, 해당 운영 체제에서 적절한 규칙이었을 때 소문자 파일 이름을 생성하는 데 사용되었습니다).

내부 문자 코드는 숫자가 연속되는 코드와 문자가 연속되는 코드를 갖도록 선택되었습니다 (최소한 그 시대의 일반적인 기계 문자 세트 중 하나인 EBCDIC는 이러한 속성을 갖고 있지 않았습니다). 이것은 MATLAB 표현식 ‘A’: ‘Z’가 항상 모든 문자를 순서대로 포함하고 다른 문자는 포함하지 않는 길이가 26인 행 벡터를 생성하는데 사용되었습니다 - 또 다른 중요한 이식성(portability)의 기여입니다.

2.5 문법 다이어그램

언어의 공식적인 정의 및 구문 분석기-인터프리터를 위한 흐름 차트 유형은 11개의 문법 다이어그램으로 제공되었습니다. 이들은 다음과 같은 열 한정자를 정의했습니다: line, statement, clause, expression, term, factor, number, integer, name, command 및 text.

간략히 말하자면, 언어의 재귀적인 핵심은 다음과 같습니다:

표현식은 + 및 - 기호로 구분된 항들입니다.
항은 * 및 / 그리고 \ 기호로 구분된 인자들입니다.
인자는 숫자, 이름 또는 괄호 ( ) 안의 표현식입니다.

1970년대에는 Fortran 프로그램이 재귀적이지 않았습니다. 이것은 실제로 하위 루틴이 자기 자신을 호출할 수 없다는 것을 의미했습니다. 따라서 원래의 MATLAB 프로그램에서는 EXPR이 TERM을 호출하고, TERM이 FACTOR를 호출하며, FACTOR는 괄호를 만나면 EXPR을 호출했습니다. 이러한 서브루틴 호출의 스택을 관리하기 위해 두 개의 배열이 필요했으며, 작업 공간의 행렬을 관리하기 위해 다른 배열이 필요했습니다.

원래의 라인 프린터 사용자 가이드에 나타난 전체 구문 다이어그램은 부록 A에서 주석을 첨부하여 제공됩니다.

2.6 사용자 함수

Classic MATLAB은 USER라는 하나의 외부 사용자 정의 함수를 허용했습니다. 사용자는 지정된 선언을 사용하여 이 함수를 Fortran으로 작성해야 했습니다.

SUBROUTINE USER(A,M,N,S,T)
REAL 또는 DOUBLE PRECISION A(M,N),S,T

이 인터페이스를 통해 MATLAB 코드는 인자의 형태와 상관없이 USER 함수를 호출할 수 있으며, 인자로는 행렬 하나와 스칼라 인자가 없거나 하나 또는 두 개가 있을 수 있으며, 행렬 하나가 반환될 것입니다. 외부 Fortran 하위 루틴이 작성된 후에는 MATLAB 인터프리터를 실행하기 전에 로컬 운영 체제 내에서 MATLAB 객체 코드와 연결하기 위해 해당 루틴을 컴파일해야 했습니다.

그림 7. MathWorks 설립자이자 CEO인 잭 리틀(Jack Little) (2000년) (출처: MathWorks)

2.7 전신들

Classic MATLAB의 가장 중요한 소프트웨어 전신들은 Algol 60과 Fortran II였습니다. Algol은 형식적인 구조를 제공하고, Wirth의 Pascal과 PL/0을 통해 구문 분석 기술을 제공했습니다. Fortran은 당시에 과학적 계산을 위한 언어로 잘 확립되어 있었습니다. LINPACK과 EISPACK은 Fortran으로 작성되었으며, IMSL 및 NAG와 같은 다른 수치 소프트웨어 컬렉션도 Fortran으로 작성되었습니다.

오늘날에는 왜 MATLAB의 인덱싱이 1을 기준으로 하는지 0을 기준으로 하는게 아닌지에 대해 의문을 제기하는 사람들도 있습니다. 이것은 Algol과 Fortran이 모두 1을 기준으로 하고 있으며, 선형 대수학 자체도 1을 기준으로 하기 때문입니다.

3. Classic MATLAB에서 상업용 제품으로의 전환

Moler는 1978년부터 1979년까지 스탠포드 대학에서 컴퓨터 과학의 초빙 교수로서 활동했습니다. 1979년 1월부터 3월까지 겨울 학기 동안 그는 석사과정생들을 대상으로 ‘고급 수치해석’ 과목을 가르치면서 자신의 간단한 행렬 계산기를 소개했습니다. 일부 학생들은 제어 이론과 신호 처리와 같은 주제를 공부하고 있었으며, Moler는 이 분야에 대해 잘 알지 못했습니다. 그러나 행렬은 이러한 주제들의 수학적 기초였고, MATLAB은 이러한 학생들에게 즉시 유용했습니다.

잭 리틀(그림 7 참조)은 스탠포드 대학의 대학원 공학 프로그램에 있었습니다. 그가 수강한 과목의 한 학생이 MATLAB을 보여주었고, 그는 즉시 제어 시스템 분야에서 자신의 작업에 MATLAB을 채택했습니다.

3.1 MathWorks MATLAB의 개발

1983년 리틀은 MATLAB을 기반으로 IBM PC용 상용 제품을 개발하는 것을 제안했습니다. Moler는 그것이 좋은 아이디어라고 생각했지만 처음에는 리틀과 함께 참여하지 않았습니다. IBM PC는 두 해 전에 도입되었으며, MATLAB과 같은 소프트웨어를 실행하는 데 거의 충분한 성능이 없었습니다. 그러나 리틀은 IBM PC의 진화를 예상하고 있었습니다. 리틀은 Intel 8087 칩을 위한 소켓을 포함하고 있었는데, 이 칩은 하드웨어에서 부동 소수점 계산을 수행했기 때문에 MATLAB에 필수적이었습니다. 그는 일자리를 그만두고 Sears에서 Compaq PC 클론을 구입한 후, Stanford 뒤의 언덕으로 이사해 MATLAB의 새로운 확장 버전을 만드는 데 1년 반을 보냈습니다. 이 컴퓨터는 256kB의 메모리와 하드 디스크가 없었으며, 프로그램을 컴파일하려면 5-1/4인치 플로피 디스크를 교체해야 했습니다. 리틀은 몰러의 Fortran을 포함하여 EISPACK과 LINPACK 루틴들을 모두 C로 다시 작성하는 작업을 수행했습니다. 친구인 Steve Bangert가 프로젝트에 합류하여 여가 시간에 새로운 MATLAB에 대해 작업했습니다. 리틀과 Bangert는 샌프란시스코 반도에서 몇 마일 떨어진 곳에 살고 있었습니다. 그들은 정기적으로 서로 만나서 최신 버전의 소프트웨어를 교환했습니다. Steve는 파서와 인터프리터를 작성하고, Jack은 수학 라이브러리를 작성했으며, 여기에는 LINPACK 및 Classic MATLAB의 약 12개 루틴을 Fortran에서 C로 변환하는 작업이 포함되었습니다. Jack은 또한 최초의 Control System Toolbox를 작성했습니다.

리틀, Bangert, Moler은 1984년 12월 7일 금요일에 캘리포니아에서 MathWorks를 설립했습니다. 이것은 1983년 3월 11일 날짜의 잭 리틀의 사업 계획서였습니다. 이 계획서에는 다음과 같이 기술되어 있습니다.

"이 간단한 노트는 기술적인 소프트웨어 제품군에 대한 설명입니다. 이 제품군의 시장은 과학 및 기술 커뮤니티입니다. 1) 마우스와 창, 2) 행렬 및 APL 환경, 그리고 3) 직접 조작 기술의 결합은 엔지니어들에게 비즈니스 분야에 대해 Lotus 1-2-3이 한 것과 같은 혁신을 가져올 것입니다. UNIX 환경을 위한 제품이기 때문에 이 소프트웨어는 가장 큰 대상 기계 기반을 확보하고 있습니다. 이 제품은 오래 지속될 가능성이 밝습니다. 커널은 많은 수직적 제품군의 기반이 됩니다. 엔지니어링 시장을 점령하는 데 더 적절한 접근 방법은 없을 것입니다."

PC-MATLAB은 다음 주에 라스베이거스에서 개최된 제23회 IEEE Decision and Control 컨퍼런스에서 처음으로 선보였습니다. 1985년 초, 첫 판매가 진행되었고 매사추세츠 공과대학교의 닉 트레페튼 (현재 옥스퍼드 대학교 소속) [Trefethen 2000, xiii쪽]에게 판매되었습니다. 닉 트레페튼은 후에 Spectral Methods in MATLAB이라는 책을 쓰기도 하고 최근에는 MATLAB 기반의 Chebfun 소프트웨어 프로젝트의 창조와 개발에 관여했습니다.

Fortran을 C로 전면적으로 다시 작성하는 과정에서 리틀과 Bangert는 많은 중요한 수정과 개선을 하였고, 새로운 확장 버전을 만들었습니다. 이 버전과 바로 뒤 이어지는 버전들을 MathWorks MATLAB로 지칭할 것입니다. 가장 중요한 혁신은 함수, 툴박스 및 그래픽 영역에서 이루어졌습니다. PC-MATLAB의 전체 내용은 [na Moler 2018e]에서 확인할 수 있습니다. PC-MATLAB은 곧 Pro-MATLAB으로 이어졌으며, 1986년에 Unix 워크스테이션에 나왔습니다. 당시에는 이러한 시스템을 생산하는 제조업체가 적어도 여섯 개 이상이 있었습니다. 가장 중요한 회사는 Sun Microsystems였습니다. 그 다음 해에는 MATLAB이 Apple Macintosh에서 사용 가능해졌습니다.

3.2 함수

1980년대 중반에는 PC, Mac 및 Unix 워크스테이션에서 다양한 운영 체제가 사용되었지만, 이들 모두 어떤 형태의 계층적 파일 시스템을 가지고 있었습니다. MATLAB 함수 명명 메커니즘은 이러한 기본 컴퓨터 파일 시스템을 사용합니다.

PC-MATLAB은 스크립트 및 함수를 통해 확장 가능하게 만들어졌습니다. (이 기능은 Classic MATLAB의 단일 USER 함수를 대체했습니다. - 섹션 2.6 참조) 스크립트 또는 함수는 확장자 “.m”을 가진 파일에 저장된 MATLAB 코드 본문입니다. (당시에는 이러한 파일들을 “M 파일”이라고 불렀지만, 오늘날에는 그 용어가 사용되지 않습니다.) 파일 내용이 function으로 시작한다면, 함수입니다. 그렇지 않으면 스크립트입니다. 파일 이름에서 .m을 제외한 부분이 스크립트 또는 함수의 이름이 됩니다. 예를 들어, hello.m이라는 파일에 다음과 같은 한 줄을 포함하면

disp('Hello World')

이것은 MATLAB 스크립트입니다. 명령 프롬프트에서 .m 확장자를 제외한 파일 이름을 입력하면,

hello

아래와 같은 전통적인 인사말을 출력합니다.

Hello World

함수는 일반적으로 입력 및 출력 인수가 있습니다. 다음은 모든 초등학교 학생들이 익숙한 곱셈 표를 생성하기 위해 벡터 외적을 사용하는 간단한 예제입니다.

function T = mults(n)
j = 1:n;
T = j'*j;
end

(이 함수의 두 문장이 모두 세미콜론으로 끝나는 것에 주의하세요. 이는 계산된 값이 출력되지 않아야 함을 나타냅니다.) 다음 문장은 5x5 곱셈 표를 생성합니다.

T = mults(5)
T =
2 3 4 5
4 6 8 10
6 9 12 15
8 12 16 20
10 15 20 25

MATLAB 함수의 입력 인수는 “값으로 전달”되며, 이는 함수가 호출자로부터 인수를 복사한 것처럼 동작한다는 것을 의미합니다. 이로 인해 함수 동작에 대한 간단하고 직관적인 정신적 모델이 형성됩니다. 그러나 메모리 효율성을 위해 MATLAB은 “복사 알아서” 동작도 구현합니다. 이 동작은 메모리 복사를 미루고 종종 실제로는 이루어지지 않습니다. 예를 들어, 이 함수는 입력 인수 A와 B의 “복사본”을 변경하지 않으므로, 함수가 호출될 때 실제로 메모리 복사가 발생하지 않습니다.

function C = commutator(A,B)
C = A*B - B*A;
end

MATLAB 코드로 정의된 함수는 내장 함수와 마찬가지로 하나 이상의 값을 반환할 수 있습니다. 하나 이상의 값을 반환하는 함수를 호출할 때, 사용자는 문장을 사용하여 다중 값을 여러 변수에 할당할 수 있습니다.

3.3 컴파일된 코드의 동적 링킹

PC-MATLAB은 Fortran 및 C 프로그램을 작성하고 컴파일한 다음 MATLAB로 동적으로 로드하여 실행할 수 있는 외부 인터페이스를 도입했습니다. 각각의 외부 함수는 “mex 파일”이라고 불리는 별도의 파일에 저장되었습니다. (현재는 일반적으로 “MEX 파일”이라고 쓰는 용어입니다.) 이 인터페이스에는 Fortran 및 C 프로그램이 배열 인수의 차원을 결정하고 실수 및 허수 부분을 찾고 결과 배열을 구성하는 등의 작업을 수행할 수 있도록 라이브러리 함수와 관련된 헤더 파일이 포함되어 있었습니다. 일반적인 mex 파일에는 “래퍼” 코드가 포함되어 있어 MATLAB 데이터 구조를 읽고 그들의 조각들을 찾아서 MATLAB 결과를 조립하며, 이와 함께 하나 이상의 코어 함수가 포함되어 있었습니다. 이 코어 함수들은 기존의 Fortran 또는 C 애플리케이션에서 작은 수정 없이 재사용되는 경우가 많았습니다. [Johnson and Moler 1994, pages 120–121]

Mex 파일은 MATLAB 코드 파일과 같은 방식으로 작동했습니다. 인터프리터의 검색 경로에 xxx.mex라는 파일이 있으면, 그것은 함수 xxx의 정의로 간주되었습니다. (실제로 정확한 접미사는 아키텍처와 운영 체제에 따라 다르며, 예를 들어 Sun 4 워크스테이션의 경우 mex4 접미사가 사용되었습니다.) MATLAB 코드 파일과 적절한 mex 파일이 모두 존재하는 경우, MATLAB 파일보다는 mex 파일이 사용되었습니다. (이 사실은 첫 번째 MATLAB 컴파일러가 구축될 때 특히 중요해졌습니다. - 섹션 4.4 참조) [Johnson and Moler 1994, pages 121]

3.4 언어 변경 및 확장

PC-MATLAB에서는 MATLAB 내부 문자 코드의 사용을 중단하고 ASCII를 문자 집합으로 채택했습니다. 이로 인해 각종 리스트를 생성하는 데 사용되는 대괄호 ‘[]’가 항상 사용되었습니다. 이외에도 이름은 대소문자를 구분하는 경우가 발생했습니다 (소문자를 입력할 때 대문자로 변환하는 대신에). 그러나 사용자는 case sensitivity를 “끄는” 함수 casesen을 도입하여 이러한 변화를 조정할 수 있었습니다. 내장 함수와 명령어의 “공식적인 철자”가 소문자로 변경되었습니다.

PC-MATLAB에서는 이름이 더 이상 네 개의 유효 문자로 제한되지 않았습니다. diary, print, rcond, roots, round, schur 등 특정 함수의 이름은 이제 공식적으로 다섯 개의 문자로 구성되었습니다.

>expression<을 사용한 “매크로 치환” 기능은 폐기되었으며, 이 기능은 함수 eval로 대체되었습니다.

클래식 MATLAB에서 지수 연산 (행렬 거듭제곱)에 사용되는 ** 연산자는 PC-MATLAB에서 ^ 로 대체되었으며, 해당 연산자에 대응하는 .^ 연산자가 요소별 거듭제곱을 나타내도록 도입되었습니다.

크로네커 텐서 곱 및 나눗셈 연산자인 .*. 및 .\., ./.은 제거되었습니다 (하지만 크로네커 텐서 곱 함수 kron은 유지되었습니다).

클래식 MATLAB에서는 여집합 (복소수 공액) 행렬 전치를 나타내기 위해 작은 따옴표 '' 가 사용되었습니다. PC-MATLAB에서는 행렬 전치를 나타내기 위해 ` .` 가 도입되었으며 복소수 공액 없이 행렬을 전치하기 위해 사용되었습니다.

PC-MATLAB에서는 논리 NOT 연산자로 ~ 접두사를 도입했으며, <>를 ~=로 “같지 않음” 비교 연산자로 대체했습니다.

PC-MATLAB에서는 while, if, 또는 elseif 절의 조건이 단일 비교 연산이 아닌 모든 표현식이 될 수 있도록 허용했습니다.

3.5 새로운 함수들

다음은 버전 1.3의 PC-MATLAB에 새롭게 추가된 기능들에 대한 간략한 요약입니다. 1981년의 고전적인 MATLAB [na Moler 2018e]과 비교하였습니다:

기본 수학 함수: fix (소수점을 버리는 함수), rem (나머지 계산 함수), sign (부호 함수), tan (탄젠트 함수), asin (아크사인 함수), acos (아크코사인 함수), atan2 (4분면 아크탄젠트 함수), log10 (상용로그 함수), bessel (베셀 함수)
속성 및 배열 조작 함수: max (벡터 내 최대값), min (벡터 내 최소값), cumsum (벡터 요소들의 누적 합), cumprod (벡터 요소들의 누적 곱), mean (벡터의 평균값), median (벡터의 중앙값), std (벡터의 표준편차), length (벡터의 길이), sort (정렬), find (논리값에 해당하는 배열 인덱스 찾기), hist (히스토그램)
배열 생성 함수: invhilb (역 힐버트 행렬 생성), zeros (모든 요소가 0인 배열 생성)
행렬 함수: expm (행렬 지수 함수), logm (행렬 로그 함수), sqrtm (행렬 제곱근 함수), funm (임의의 행렬 함수)
다항식 함수: polyval (다항식 평가)
신호 처리 함수: filter (디지털 필터), fft (빠른 푸리에 변환), ifft (역 빠른 푸리에 변환), conv (합성)
플로팅 (이미 있는 Classic MATLAB의 plot 함수 보완): shg (그래픽 화면 표시), cla (현재 축 지우기), clg (그래픽 화면 지우기), loglog (로그로그 X-Y 그래프), semilogx (반로그 X-Y 그래프), semilogy (반로그 X-Y 그래프), polar (극 좌표 그래프), mesh (3차원 메쉬 표면), title (그래프 제목), xlabel (X축 레이블), ylabel (Y축 레이블), grid (그리드 라인 그리기), axis (수동 축 스케일링), disp (간략한 행렬 표시)
“시스템” 연산: eval (변수의 텍스트 해석), setstr (행렬이 문자열임을 나타내는 플래그 설정), exist (변수 또는 함수의 존재 확인), demo (데모 실행), pack (메모리 가비지 수집 및 압축)

이러한 새로운 함수들은 MATLAB의 기능을 크게 확장하여 다양한 응용 분야에서 보다 강력하고 다재다능한 사용이 가능하도록 하였습니다.

3.6 툴박스

MATLAB에서 사용자 정의 함수를 지원하는 기능은 MATLAB 코드나 Fortran 및 C 코드로 된 mex 파일로 구현할 수 있도록 하였습니다. 이러한 기능과 함께 발전하는 운영 체제에서 지원하는 계층적 파일 시스템은 MATLAB을 툴박스로 구성하는 것이 가능하게 만들었습니다. 툴박스는 특정 응용 분야에 특화된 함수들의 모음으로 구성되어 있습니다. 이러한 기능은 MATLAB의 진화에 있어서 핵심적인 역할을 담당하게 되었습니다. 첫 번째 툴박스인 MATLAB 툴박스는 인터프리터에 내장되지 않은 모든 수학 및 일반 함수를 구현했습니다.

잭 리틀은 제어 및 신호 엔지니어이기도 합니다. 따라서 1985년에 Control System Toolbox의 첫 버전을 작성하여 출시하였습니다. 그리고 MathWorks의 세 번째 직원인 Loren Shure와 함께 1987년에 Signal Processing Toolbox의 첫 버전을 작성하였습니다.

두 명의 외부 학계 저자가 자신들의 분야 전문성을 바탕으로 초기 툴박스를 작성했습니다. 스웨덴의 링쇼핑 기술 연구소 교수인 Lennart Ljung은 1988년 System Identification Toolbox [Ljung 2014; na Ljung 2012b; na Ljung 2012a]를 그의 광범위하게 사용되는 교재와 함께 사용하기 위해 작성했습니다 [Ljung 1987]. 또한 위스콘신 대학교 매디슨 캠퍼스의 Carl de Boor 교수는 1990년에 Spline Toolbox [de Boor 2004]를 작성했습니다. 이 툴박스는 현재의 Curve Fitting Toolbox의 전신으로 사용되었으며, 그의 B-스플라인에 관한 권위있는 책과 함께 사용되었습니다 [De Boor 1978].

3.7 그래픽스

기술적인 컴퓨터 그래픽스는 처음부터 MATLAB의 핵심적인 부분이었습니다. 많은 사용자들이 MATLAB의 플로팅 기능 때문에 이용합니다. 사용자들은 물리적 실험이나 다른 소프트웨어 계산으로부터 데이터를 얻습니다. MATLAB은 보고서나 기술 논문에 적합한 플롯을 생성합니다.

배열에 대한 작업은 메모리 맵드 그래픽스에 편리했습니다. 배열 데이터 유형은 2차원(X-Y) 및 3차원(X-Y-Z) 차트에 자연스러웠습니다. 그러나 심지어 1981년 버전의 클래식 MATLAB에는 원시적인 플롯 함수가 있었는데 이는 “ASCII 플롯”을 생성했습니다 (그림 8 참조). 오늘날의 MATLAB은 동일한 함수에 대해 더 세련된 플롯을 생성합니다 (그림 9 참조).

그림 8. 이 휴대용 기계 독립적인 그래프는 클래식 MATLAB의 일부이며, 부분적으로 농담이었지만 미래의 그래픽 기능에 대한 예상이었습니다.

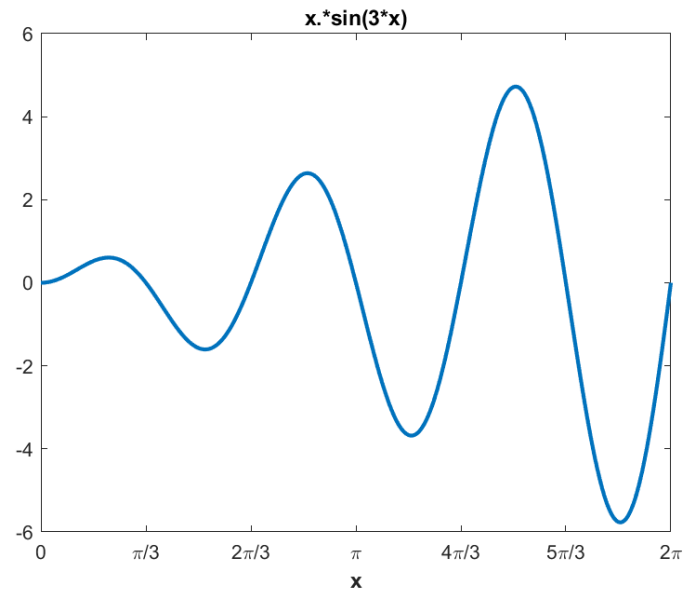
그림 9. 동일한 함수에 대한 현대적인 MATLAB으로 생성된 그래프

캘리포니아 대학교 산타 바바라 캠퍼스의 교수인 Marvin Marcus가 저술한 교과서 “Matrices and MATLAB”은 Macintosh-IIci에서 개발되었으며 초기 컴퓨터 그래픽스를 이용했습니다 [Marcus 1993]. 그림 10은 𝑓(𝑧) = 𝑧2 + 𝑐 함수의 Julia 집합을 𝑐 = 0.1 + 0.8𝑖로 MATLAB이 그린 그래프입니다. 오늘날의 MATLAB로 그려진 플롯에서는 훨씬 더 많은 세부 사항이 보입니다 (그림 11 참조).

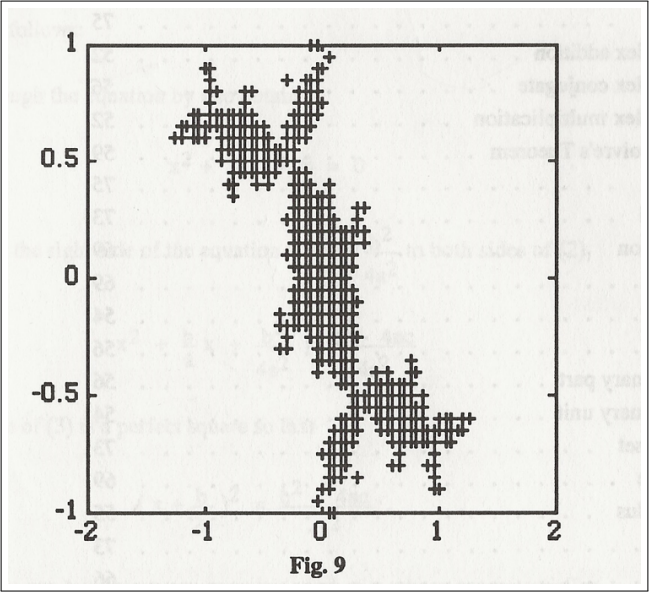
그림 10. 1992년에 Marvin Marcus [Marcus 1993]가 Apple Macintosh IIci에서 MATLAB으로 생성한 줄리아 집합의 그래프입니다. (출처: Prentice Hall)

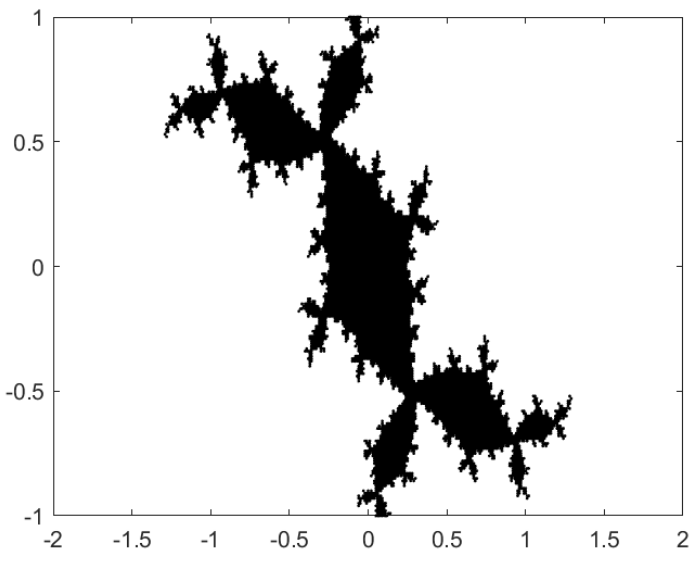
그림 11. 동일한 줄리아 집합의 그래프로 현대적인 MATLAB으로 생성한 것입니다.

3가지 더 예제를 살펴봅시다. 이들은 모두 수치 선형 대수와는 관련이 없지만 모두 벡터 표기법과 배열 연산을 사용합니다.

다음 코드는 그림 12에 표시된 플롯을 생성합니다:

x = -pi:pi/1024:pi;
y = tan(sin(x))-sin(tan(x));
plot(x,y)
xlabel('x')
title('tan(sin(x)) - sin(tan(x))')

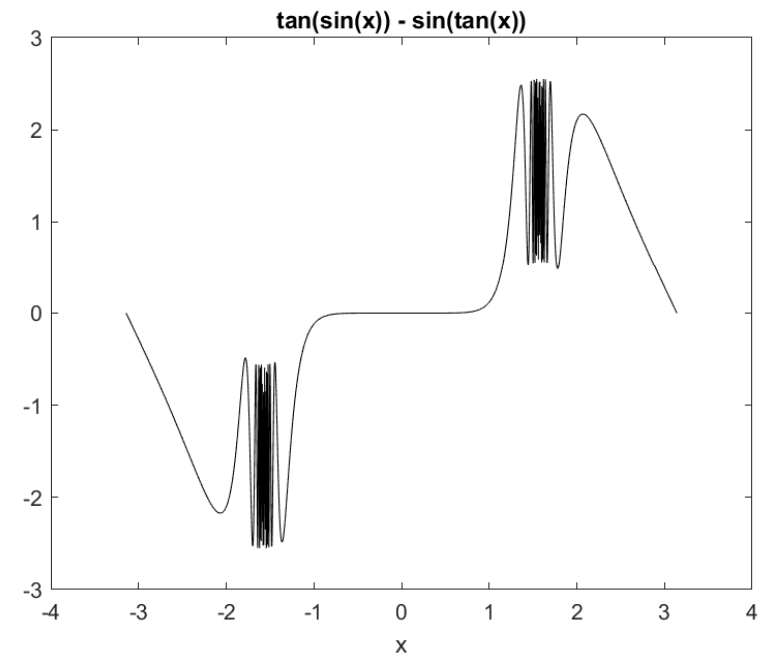
그림 12. 현대적인 MATLAB으로 생성한 2차원 플롯

다음 코드는 그림 13에 표시된 플롯을 생성합니다:

X = (-3:1/8:3)*ones(49,1);
Y = X';
Z = 3*(1-X).^2.*exp(-(X.^2) - (Y+1).^2) ...
- 10*(X/5 - X.^3 - Y.^5).*exp(-X.^2-Y.^2) ...
- 1/3*exp(-(X+1).^2 - Y.^2);
mesh(X,Y,Z)

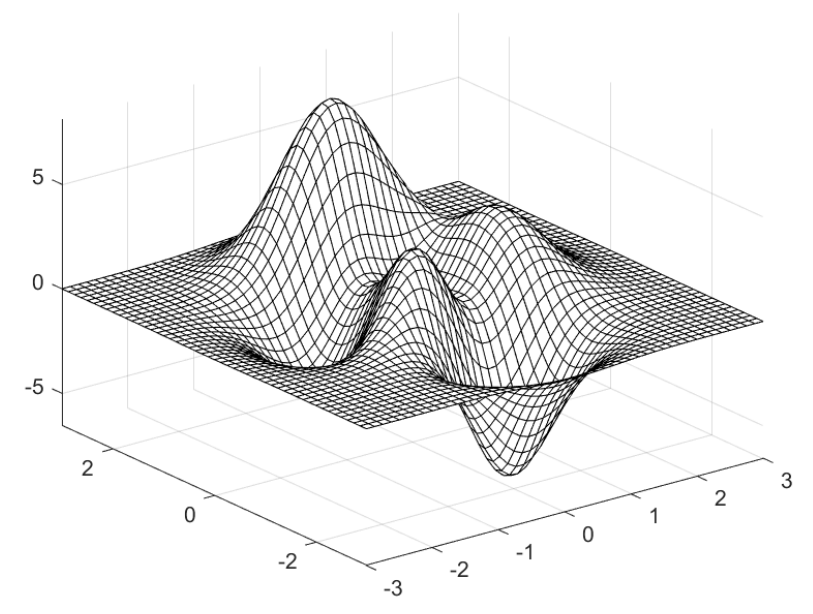
그림 13. 현대적인 MATLAB으로 생성한 3차원 플롯

Control System Toolbox에서 Bode 다이어그램은 동적 시스템의 주파수 응답을 보여줍니다 (그림 14 참조).

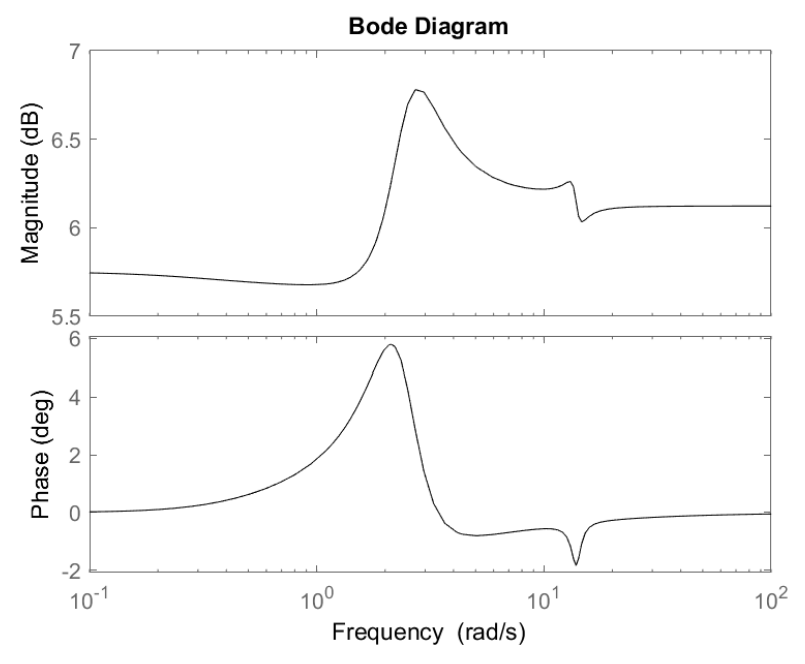
그림 14. 컨트롤 시스템 툴박스의 보데(Bode) 플롯은 시스템의 주파수 응답의 크기와 위상 이동을 보여줍니다.

1988년, Moler는 MATLAB을 단순히 “행렬 연구소”뿐만 아니라 “수학적 시각화 연구소”로 묘사했습니다 [Moler 1988].

3.8 Flops Count

클래식 MATLAB 인터프리터는 수행된 모든 부동 소수점 연산(“flop”)을 카운트하고, 문장이 추가적인 쉼표로 종료되면 해당 카운트를 보고했습니다. 이 기능은 MathWorks MATLAB으로 이어졌지만, 현재의 MATLAB에서는 행렬 및 기타 계산의 내부 루프가 가능한한 효율적이어야 하기 때문에 사용할 수 없습니다. 그림 15는 𝑛-by-𝑛 행렬의 역행렬을 구하는 것이 약 $n^3$개의 부동 소수점 연산을 필요로 한다는 사실을 보여주는 데모입니다. (1984년 버전의 MATLAB으로 제작되었습니다).

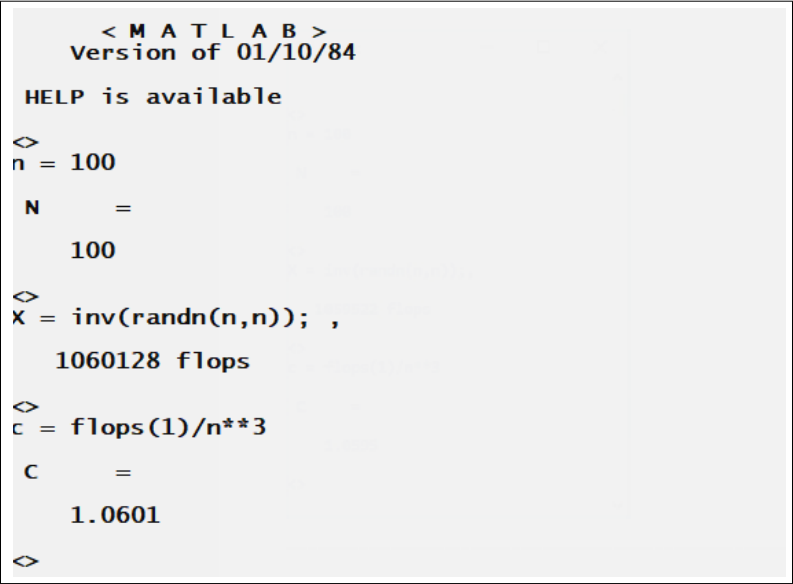
그림 15. 클래식 MATLAB에서 추가 쉼표를 사용하여 flops(부동 소수점 연산 수)를 출력하는 방법을 보여주는 데모입니다.

flops 카운트는 또한 flop 변수로 사용자에게 제공되었습니다. 이 변수는 1-by-2 행렬로, 첫 번째 항목은 바로 이전 입력에서 수행된 flops의 수이고, 두 번째 항목은 첫 번째 항목이 취한 값들의 누적 합(포함적)입니다. MATLAB의 이후 버전에서는 flops 함수가 소개되어 flop 카운트를 반환하고 초기화하는 데 사용되었습니다.

flop 카운트를 추적하고 보고하는 기능은 EISPACK과 LINPACK에서 적용된 루틴들이 LAPACK으로 대체되면서(Section 5.1 참조) 지원이 중단되었습니다.

4. MATLAB의 진화

MATLAB은 행렬 수학의 기본 원리를 유지하면서 엔지니어와 과학자들의 변화하는 요구를 충족하기 위해 지속적으로 진화해왔습니다. 다음은 주요한 발전 과정들입니다 [na Moler 2018c; na Moler 2018d].

4.1 데이터 타입

1992년에는 MathWorks는 100명 이상의 스태프를 보유하고, 1995년에는 200명 이상이었습니다. 그 중 약 절반이 과학 및 공학 학위를 가지고 있으며 MATLAB과 각종 툴박스의 개발에 참여하고 있었습니다. 그들은 MATLAB 프로그래머들의 큰 그룹으로서 풍부한 경험을 지니고 있었습니다. 회사 내부에서는 이러한 사용자들로부터 언어 개선에 대한 제안이 종종 나왔습니다.

MATLAB은 디자인과 모델링에 사용되는 임베디드 시스템에 대해 사용되고 있었습니다. 임베디드 시스템은 더 큰 전기 또는 기계 시스템 내에서 특정 실시간 기능을 갖는 컨트롤러입니다. 이러한 컨트롤러들은 종종 단일 정밀도 부동 소수점 또는 고정 소수점 산술만을 사용합니다. 임베디드 시스템의 설계자들은 대상 프로세서의 기본 산술을 사용하여 알고리즘을 개발하기를 원했습니다. 이로 인해 MATLAB에 여러 새로운 데이터 타입이 도입되었습니다만, 실제 타입 선언은 사용되지 않았습니다.

많은 해 동안, MATLAB은 IEEE 표준 754 이중 정밀도 부동 소수점을 포함한 하나의 숫자 데이터 타입만을 가졌으며, 64비트 형식으로 저장되었습니다.

format long
phi = (1 + sqrt(5))/2

phi =
    1.618033988749895

이중 정밀도 이외의 숫자 데이터 타입에 대한 지원은 1996년부터 2004년까지 점진적으로 MATLAB에 추가되었습니다. 단일 정밀도 부동 소수점은 32비트 저장 공간만을 요구하며, 큰 배열의 메모리 요구 사항을 절반으로 줄일 수 있습니다. 이것이 더 빠를 수도 있고 그렇지 않을 수도 있습니다.

MATLAB은 선언문이 없기 때문에, 단일 정밀도 변수는 실행 가능한 변환 함수를 통해 이중 정밀도 변수로부터 얻어집니다.

p = single(phi)
p =
    single
    1.6180340

처음에는 uint8와 uint16과 같은 부호 없는 정수 타입은 이미지 저장에만 사용되었습니다. 산술 연산이 필요하지 않았습니다.

2004년 MATLAB 7에서는 단일 정밀도에 대한 완전한 산술 지원을 도입했으며, 네 가지의 부호 없는 정수 데이터 타입 (uint8, uint16, uint32 및 uint64)과 네 가지의 부호 있는 정수 데이터 타입 (int8, int16, int32 및 int64)을 지원했습니다. 또한 MATLAB 7에서는 새로운 논리 타입을 도입했습니다.

q = uint16(1000*phi)
r = int8(-10*phi)
s = logical(phi)
q =
    uint16
    1618
r =
    int8
    -16
s =
    logical
    1

각각의 변수들을 저장하는데 얼마만큼의 용량이 드는지 확인해봅시다.

Name Size Bytes Class
p    1x1  4     single
phi  1x1  8     double
q    1x1  2     uint16
r    1x1  1     int8
s    1x1  1     logical

4.2 희소 행렬

행렬 계산의 관례적인 이야기에 의하면, J.H. 윌킨슨은 희소 행렬을 “0의 개수가 충분하여 이점을 취할 수 있는 모든 행렬”로 정의했습니다. (실제로 그는 그의 학생들에게 정확히 이렇게 말했을지도 모르지만, 이것은 자동 계산을 위한 핸드북에 쓴 이 문장과 비교해야 합니다:

iv) 행렬은 희소할 수 있으며, 0이 아닌 요소들이 대각선을 중심으로 좁은 대역에 집중되어 있을 수도 있고, 덜 체계적인 방식으로 분포되어 있을 수도 있습니다. 우리는 이러한 행렬을 0 요소의 비율이나 분포로 인해 이용하는 것이 경제적이지 않은 경우에 밀집된(dense) 행렬이라고 할 것입니다.

[Wilkinson and Reinsch 1971, page 191].)

Iain Duff는 희소 행렬 계산을 위한 알고리즘 및 소프트웨어에 대한 연구로 잘 알려진 영국의 수학자 및 컴퓨터 과학자입니다. 1990년에 그는 스탠포드를 방문하여 수치 해석 세미나에서 강연을 하였습니다. Moler도 이 강연을 듣고 있었습니다. 그리고 Xerox Palo Alto Research Center에 있던 John Gilbert과 Hewlett Packard Research에 속한 Rob Schreiber도 함께 강연을 들으러 갔습니다. 그들은 스탠포드의 Tresidder Union에서 점심을 먹으며 Gilbert, Schreiber 및 Moler는 MATLAB에서 희소 행렬을 지원할 때가 되었다고 결정하였습니다.

1992년 MATLAB 4에서는 희소 행렬이 도입되었습니다. 여러 가지 디자인 옵션과 원칙들이 탐구되었습니다. 행렬의 값과 해당 행렬을 위해 사용되는 특정 표현 사이에 명확한 구분을 그리는 것이 중요했습니다. [Gilbert et al. 1992, page 4]:

행렬과 그것이 가진 저장 클래스 사이의 차이점을 강조하고자 합니다. 하나의 행렬은 여러 가지 방식으로 저장될 수 있습니다 - 고정 소수점 또는 부동 소수점, 행별 또는 열별로, 실수 또는 복소수, 전체 행렬(full matrix) 또는 희소 행렬(sparse matrix) - 하지만 이러한 다양한 방식들은 모두 같은 행렬을 나타냅니다. 이제 MATLAB에는 full과 sparse 두 가지 행렬 저장 클래스가 있습니다.

네 가지 중요한 디자인 원칙이 나타났습니다.

연산의 결과 값은 피연산자의 저장 클래스에 의존해서는 안 되지만, 결과 값의 저장 클래스는 영향을 받을 수 있습니다. [Gilbert et al. 1992, 페이지 10]
사용자의 명시적 지시 없이는 희소 행렬을 생성해서는 안 됩니다. 따라서 MATLAB의 변경 사항은 희소성이 필요하지 않은 사용자에게 영향을 미치지 않아야 합니다. 전체 행렬에 대한 연산은 여전히 전체 행렬을 생성합니다.
희소성이 시작되면 전파됩니다. 희소 행렬에 대한 연산은 희소 행렬을 생성하며, 희소 행렬과 전체 행렬의 혼합에 대한 연산은 연산자가 희소성을 파괴하지 않는 한 희소 결과를 생성합니다. [Gilbert et al. 1992, page 5]
희소 행렬 연산에 필요한 컴퓨터 시간은 0이 아닌 요소들의 산술 연산 횟수에 비례해야 합니다. [Gilbert et al. 1992, page 3] (이러한 원칙 중 일부는 나중에 단일 정밀도와 정수형 지원을 추가하는 디자인 노력에서 다시 발견되었습니다.)

희소 행렬은 0이 아닌 요소들만 저장하며, 해당하는 행 인덱스와 열의 시작 위치를 포함합니다. MATLAB의 외부 모습에 유일한 변화는 사용자가 행렬을 제공하고 지정된 저장 클래스를 가진 사본을 얻을 수 있는 sparse와 full 두 개의 함수가 추가된 것입니다. 거의 모든 다른 연산은 전체 행렬과 희소 행렬 모두에 적용됩니다. 희소 행렬 저장 방식은 0이 아닌 항목의 개수에 비례하여 행렬을 표현하며, 대부분의 연산은 0이 아닌 항목에 대한 산술 연산의 개수에 비례하여 희소 결과를 계산합니다. 또한, 희소 행렬은 0이 아닌 항목만 출력하는 다른 형식으로 출력됩니다.

예를 들어, 라플라시안 미분 연산자에 대한 클래식한 유한 차분 근사법을 고려해 봅시다. numgrid 함수는 이차원 격자에서 점들을 번호 매기는데, 이 경우에는 정사각형 내부의 n-by-n 점들을 번호 매깁니다.

n = 100;
S = numgrid('S', n+2);

delsq 함수는 희소 행렬로 저장되는 N-by-N 크기의 다섯점 이산 라플라시안을 생성합니다. 여기서 N = n^2 입니다. 각 행마다 다섯 개 이하의 0이 아닌 요소를 가지므로, 전체 0이 아닌 요소의 총 수는 약 5N보다 조금 작습니다.

A = delsq(S);
nz = nnz(A);

nz에는 49600이 저장되어 있습니다.

비교를 위해 행렬의 전체 버전을 생성하고 필요한 저장 공간을 확인해 봅시다. A의 저장 공간은 N에 비례하며, F의 저장 공간은 N^2에 비례합니다.

F = full(A);

F의 크기는 10000x10000이며 저장 공간은 800,000,000 바이트로 double 클래스를 가지는 풀 행렬입니다.

경계값 문제에 대한 해를 계산하는 데 걸리는 시간을 측정해 봅시다. 희소 행렬의 경우 시간 복잡도는 O(N^2)입니다. n = 100이고 N = 10000인 경우, 해를 계산하는 데 걸리는 시간은 즉시 계산됩니다.

b = ones(n^2, 1);
tic
u = A\b;
toc

소요 시간은 0.029500초입니다.

풀 행렬의 경우 시간 복잡도는 O(N^3)입니다. 동일한 해를 계산하는 데 몇 초가 걸립니다.

tic
u = F\b;
toc

소요 시간은 7.810682초입니다.

4.3 빈 행렬

클래식한 MATLAB에는 크기가 0 × 0인 빈 행렬 하나만 있었습니다. 이는 <> (또는 []로 시작하는 MathWorks MATLAB)로 표시됩니다. 그러나 Carl de Boor의 더 정확한 분석 [de Boor 1990] (이 분석은 일부로부터 영감을 받은 APL에 대한 유사한 작업에 의존했습니다)으로 인해 MATLAB에서는 모든 크기의 빈 행렬을 지원해야 한다는 결론에 이르렀습니다. 즉, 비음이 아닌 모든 𝑛에 대해 크기가 𝑛 × 0 및 0 × 𝑛인 빈 행렬을 지원합니다. (또한 배열이 도입될 때는 가능한 모든 모양의 빈 배열도 지원되었습니다.)

빈 행렬은 몇 가지 놀라운, 그러나 논리적으로 일관된 특성을 가지고 있습니다.

x = ones(4, 0)
x =
  4x0 empty double matrix

빈 열 벡터와 동일한 길이의 빈 행 벡터의 내적은 빈 행렬입니다.

z = x' * x
z =
  []

빈 열 벡터와 동일한 길이의 빈 행 벡터의 외적은 모두 0으로 채워진 풀 행렬입니다. 이는 빈 합이 0임을 반영하는 규칙으로부터 나온 결과입니다.

y = ones(0, 5)
A = x * y
y =
  0x5 empty double matrix
A =
  0 0 0 0 0
  0 0 0 0 0
  0 0 0 0 0
  0 0 0 0 0

de Boor가 관찰한 바와 같이, 빈 행렬을 사용하는 한 가지 방법은 반복적 또는 귀납적인 행렬 알고리즘의 적절한 기본 사례(또는 종료 사례)를 제공하여 초기 또는 최종 사례의 처리가 별도의 코드를 필요로하지 않도록 하는 것입니다.

4.4 MATLAB의 컴파일

1990년대 초, 스티븐 C. “스티브” 존슨은 yacc [na Johnson 1975], lint [na Johnson 1978], 그리고 Portable C Compiler [Johnson 1978; na Johnson 1979] 등의 작업으로도 알려진 인물로, MATLAB의 첫 번째 컴파일러를 구축했습니다. 이 컴파일러는 1994년 논문 [Johnson and Moler 1994]에 설명되었으며, 1995년에 발표되었습니다.

MATLAB 컴파일러를 MATLAB 인터프리터와 연결하기 위한 많은 인프라가 이미 구축되어 있었습니다. 사용자가 정의한 MATLAB 함수는 이미 별도의 소스 코드 파일에 저장되어 있었고(3.2절 참조), 컴파일된 코드 파일을 동적으로 로드할 수 있는 mex파일에 대한 기능도 이미 있었습니다(3.3절 참조). 또한, 동일한 함수에 대해 소스 코드 파일과 컴파일된 파일이 이미 존재한다면, MATLAB 인터프리터는 컴파일된 파일을 사용합니다. 따라서 MATLAB 컴파일러는 MATLAB 코드 파일을 읽고 해당하는 컴파일된 mex파일을 생성하는 것이었습니다.

많은 MATLAB 함수는 이미 큰 행렬에 EISPACK와 LINPACK 행렬 연산을 적용하여 인터프리터에서 적절한 속도로 실행되었습니다. 하지만 일부 코드는 스칼라 연산을 필요로 했습니다. 예를 들어, 삼중 대각 선형 방정식을 해결하는 경우, 전체 행렬 연산을 사용하여 해를 구할 수 있지만 시스템 크기에 대해 이차적인 비용이 발생합니다. 또는 MATLAB 프로그래밍 언어로 작성된 사용자 함수에서 루프를 사용하는 대안으로 시스템 크기에 대해 선형적인 비용이 발생하지만, 개별 스칼라 연산의 인터프리터 오버헤드와 관련된 큰 상수 배수가 곱해집니다. MATLAB 컴파일러는 이러한 삼중 대각 선형 방정식 해결기의 실행 속도를 개선했습니다. 예를 들어, 크기가 1000인 시스템에 대해 실행 속도를 약 100배 향상시켰으며(크기가 1000인 대각선과 크기가 999인 두 개의 대각선), 크기가 5000인 시스템에 대해서는 거의 150배 향상되었습니다 [Johnson and Moler 1994].

이 첫 번째 MATLAB 컴파일러의 가장 중요한 작업은 유형 분석이었습니다. 특정 변수의 사용이나 계산된 양이 항상 비복소인가요? 항상 정수인가요? 항상 행렬보다 스칼라인가요? 이러한 질문에 대답하기 위해 컴파일러는 def-use 연결, 언어 구조 및 내장 함수에 대한 지식, 그리고 최소 고정점 유형 분석을 사용했습니다. 예를 들어, 컴파일러는 표현식 1:n이 항상 정수 배열이라는 것을 알고 있습니다. 따라서 i=1:n에 대해 변수 i는 항상 스칼라이며 항상 정수 값을 갖습니다. 이러한 정보는 i를 사용하여 표현식(특히 하위 스크립트 표현식)을 컴파일하는 것을 훨씬 더 쉽게 만들어줍니다. 예를 들어, 컴파일러가 i가 복소 행렬이 아닌 스칼라 정수라는 사실을 알고 있다면, i*i를 계산하는 것이 훨씬 간단합니다. 만약 i가 스칼라라면, i*i도 스칼라이고, 따라서 a(i*i)도 스칼라입니다(하지만 반드시 정수일 필요는 없습니다. 이는 a의 유형에 달려 있습니다). 이것은 제약 조건의 하향식 전파의 한 예입니다. 상향식 전파의 예로는 다음 코드 조각을 고려해보세요:

function a=f(x)
...
y(3) = 4 + x;
...

입력 변수 x는 미리 어떤 모양이 될 지 모를 수 있지만, 상수 3이 스칼라이기 때문에 y(3)은 필연적으로 스칼라입니다(하향식 제약), 따라서 4 + x는 스칼라여야 합니다(상향식), 그리고 따라서 해당 지점에서 x도 스칼라여야 합니다(상향식).

이 원래의 MATLAB 컴파일러는 상향식 제약과 하향식 제약을 모두 반복적으로 적용했습니다. 또한 적절한 경우 여러 함수를 재귀적으로 분석하여 처리했습니다. 컴파일러는 또한 함수 호출의 인수와 결과의 수와 유형을 검사하여 가능한 경우 오버로드된 함수를 해결했습니다.

이 컴파일러는 모든 MATLAB 함수를 컴파일할 필요가 없었습니다. 특정 함수의 유형 분석이 효율적인 코드 생성을 허용하기에 너무 어렵다면, 해당 함수의 MATLAB 소스 코드 버전은 여전히 호출 프로그램에서 사용할 수 있었습니다. 결과적으로 이 컴파일러를 사용하여 지적 재산권을 보호하려는 사람들이 더 많았으며, 빠른 실행을 기대하는 것보다 그러한 용도로 많이 사용되었습니다.

4.5 펜티엄 FDIV 버그

스티브 존슨은 다음과 같이 회상합니다[Johnson 2020]:

저는 컴파일러를 작성할 때 [캘리포니아]에서 작업하고 한 달에 한 번 정도 보스턴으로 비행하여 며칠 동안 머물렀습니다. (그 때는 MathWorks를 위해 반 몫의 시간을 할애하고, 또한 HP를 위해 컨설팅을 하면서 Itanium으로 발전한 모듈러 스케줄링 코드를 작성하고 있었습니다. 두 가지 매우 흥미로운 성공적인 프로젝트지만 기술적으로는 매우 다른 프로젝트였습니다.) 저는 보스턴에 있을 때는 클리브와 사무실을 공유했습니다. 어느 때는 방문했을 때, FDIV 버그가 방금 발생했고, 클리브의 전화가 끊임없이 울리기 시작했습니다. 그 때 CNN에서 인터뷰를 받은 것으로 기억합니다.

실제로 그는 인터뷰를 받았으며 Associated Press [na Press 1994], 뉴욕 타임즈 [Markoff 1994] 및 많은 다른 뉴스 매체에서도 인터뷰를 받았습니다. 인텔의 펜티엄 프로세서에는 새롭게 구현된 부동 소수점 나눗셈 명령 FDIV가 포함되었습니다. 이 명령은 Sweeney-Robertson-Tocher (SRT) 알고리즘의 변형을 사용하며, 하드웨어 조회 테이블에 2048개 항목이 있으며 이 중 절반 이상은 알고리즘이 절대로 접근하지 않는 128 × 16 테이블의 사다리꼴 모양 부분만이 사용됩니다. 불행하게도, 어떤 실수로 인해 1066개 항목 중 5개의 항목이 실제 값인 2가 아니라 0으로 설정되었습니다. 게다가 이러한 항목은 매우 드물게만 접근되며, 인텔의 무작위 테스트 과정에서 놓친 것입니다. 또한 잘못된 항목은 나눗셈 알고리즘의 처음 8단계 동안은 절대로 접근되지 않기 때문에 잘못된 결과가 진짜 결과와 약간만 차이가 납니다. 이는 고정도 계산에서 문제가 발생하지만 문제를 찾고 있는 경우나 매우 주의 깊을 때만 눈에 띄게 차이가 납니다.

하지만 Lynchburg College의 Thomas Nicely 교수는 같은 알고리즘(쌍둥이 소수의 역수 합산 계산)을 여러 컴퓨터에서 실행하고 있어서 펜티엄 기반 시스템에서 얻은 결과가 다른 결과와 다르다는 점에 주목했습니다. Nicely 교수는 불일치의 다른 가능한 이유를 몇 달간 확인한 후, 1994년 10월 24일에 인텔에 알렸으며 10월 30일에 다른 연락처에 이메일을 보냈습니다. Nicely의 메모 수신자 중 한 명이 그것을 CompuServe 네트워크에 게시했습니다. EE Times 기자인 Alex Wolfe는 이 게시물을 발견하고 노르웨이의 Norsk Hydro의 Terje Mathisen에게 보냈습니다. Wolfe의 질문을 받은 지 몇 시간만에 Mathisen은 Nicely의 예제를 확인하고 짧은 어셈블리어 테스트 프로그램을 작성하였으며, 11월 3일에 FDIV 버그에 대한 comp.sys.intel 뉴스그룹의 인터넷 게시물 체인을 시작했습니다. 하루 뒤에 독일의 Andreas Kaiser는 펜티엄에서의 단일 정밀도 정확성으로 계산된 두 수십개의 숫자 목록을 게시했습니다. [na Moler 2013d]

이야기는 Wolfe가 11월 7일에 Electronic Engineering Times에 기사로 보도함으로써 인터넷에서 빠르게 퍼졌습니다.

한편, 캘리포니아 남부의 Vitesse Semiconductor에서 부동 소수점 유닛(FPU) 디자이너인 Tim Coe는 Kaiser의 오류가 포함된 역수 목록을 보고 다른 FPU 디자이너들이 나눗셈 회로를 설계하는 과정에서 어떤 방식을 사용했는지에 대한 단서를 찾았습니다. 그는 펜티엄의 나눗셈 명령이 라디엑스-4 SRT 알고리즘을 사용하여 기계 사이클당 두 개의 비트의 몫을 생성하며, 따라서 이전 인텔 칩과 같은 클록 속도에서 펜티엄은 나눗셈이 두 배로 빨라진다는 것을 정확히 예측했습니다.

Coe는 모든 Kaiser가 보고한 역수 오류를 설명하는 모델을 만들었습니다. 또한, 분자가 하나가 아닌 다른 수를 사용하는 나눗셈 연산이 더 큰 상대적 오류를 가질 수 있다는 것을 깨달았습니다. 그의 모델은 비율이 4195835/3145727인 두 개의 일곱 자리 정수를 제시하며, 이 비율이 최악의 경우의 오류 인스턴스인 것처럼 보였습니다. 그는 이 예제를 11월 14일에 comp.sys.intel 뉴스그룹에 게시했습니다.

한편, Moler는 Coe가 게시한 몇 일 전에 FDIV 버그에 대해 다른 부동 소수점 산술에 관한 전자 메일 리스트인 David Hough가 관리하는 곳에서 처음 알게 되었습니다. 그때부터 Moler는 comp.sys.intel을 지켜보기 시작했습니다. 처음에는 호기심이 있었지만 높은 경계에 놓이지는 않았습니다. 그러나 Coe의 발견과 함께 MathWorks 기술 지원으로 몇 통의 고객 전화가 들어오면서 흥미 수준이 상당히 높아졌습니다. 11월 15일, Moler는 comp.soft-sys.matlab과 comp.sys.intel 뉴스그룹에 Nicely의 예제와 Coe의 예제를 포함하여 그 때까지 알려진 내용을 요약하고, 두 경우 모두 나누는 수가 2의 거듭제곱의 약 3배보다 조금 적다는 점을 강조하는 글을 게시했습니다.

11월 22일, Jet Propulsion Laboratory의 두 기술자들은 구매부서에게 펜티엄 칩을 장착한 컴퓨터 주문을 중단하라고 제안했습니다. CNN 기자인 Steve Young은 JPL의 결정에 대해 듣고, Moler의 뉴스그룹 게시물을 찾아 빠르게 전화를 걸고, 그 후에는 매사추세츠 MathWorks에서 비디오 크루를 보내 칼리포니아에서 그와 인터뷰를 하였습니다. 그날 저녁, CNN의 Moneyline 프로그램에서는 JPL에 대한 뉴스와 Moler의 인터뷰를 사용하여 펜티엄 나눗셈 버그를 대중적인 뉴스로 소개했습니다. 이틀 후, 다행히도 추수감사절인 그날—뉴욕 타임즈, 보스턴 글로브 [Zitner 1994], 샌호세 머큐리 뉴스 [Takahashi 1994] 등에서 이에 관한 기사들이 등장했으며, 이후 몇 주간 수백 개의 기사가 게재되었습니다.

한편, Moler는 Coe, Mathisen, Argonne National Laboratory의 Peter Tang, 그리고 인텔의 몇 명의 하드웨어 및 소프트웨어 엔지니어들과 협력하여 FDIV 버그 (그리고 펜티엄의 칩 내 탄젠트, 아크탄젠트, 나머지 명령과 관련 버그)를 해결하기 위한 소프트웨어를 개발, 구현, 테스트하고 올바르게 작동함을 입증하기 시작했습니다. 그들은 12월 5일까지 지능적인 해결책을 개발했습니다. 이 해결책은 나누는 수의 분수 부분(명시적으로 표시되는 유효 숫자 부분)의 상위 4비트를 조사합니다. 그 비트들이 0001, 0100, 0111, 1010 또는 1101인 경우, 나눗셈 연산을 수행하기 전에 피제수와 나눗수를 모두 15/16로 곱합니다. 이 다섯 가지 경우 모두 15/16로 스케일링하는 효과는 나눗셈이 위험한 패턴에서 안전한 패턴으로 변하게 됩니다. 모든 경우에서 스케일된 피연산과 나눗셈의 몫은 원래 피연산과 나눗셈의 올바른 몫과 동일합니다. 그들은 이후 몇 일 후에 이를 더 정교하게 만들어 나누는 수의 분수 부분의 상위 8비트가 00011111, 01001111, 01111111, 10101111, 11011111인 경우에만 피연산과 나눗셈을 15/16로 스케일링하는 방법을 개발했습니다. 이렇게 하면 스케일링할 경우의 수를 크게 줄일 수 있었습니다. 이 기술은 모든 사람이 자유롭게 사용할 수 있도록 뉴스그룹에 게시되었습니다.

1994년 가을에는 MathWorks는 250명 미만의 작은 회사였습니다. MATLAB이라는 제품 이름은 고객들에게 알려져 있었지만, 회사 이름인 MathWorks는 널리 알려지지 않았습니다. 11월 23일, 회사는 펜티엄 나눗셈 버그를 감지하고 수정하는 MATLAB 버전을 발표했습니다. 공공 관계 회사가 기사를 발행했으며 제목은 “The MathWorks Develops Fix for the Intel Pentium(TM) Floating Point Error”였습니다. 다음날, 이 PR 메시지가 뉴욕 타임즈와 다른 주요 신문사에 기사가 나오기 전에 미국 전역의 언론 매체의 팩스 기계에 도착했습니다. 이것은 매우 성공적인 보도 자료가 되었습니다. “Pentium Aware” 버전인 4.2c.2의 MATLAB은 1994년 12월 27일에 Windows 버전의 MATLAB 사용자에게 무료로 제공되었습니다. 이 버전은 펜티엄 나눗셈 버그를 보정하는 것뿐만 아니라, 버그를 만날 때마다 짧은 보고서를 자동으로 인쇄합니다. 또한 메시지를 억제하거나 발생 횟수를 계산하거나 보정을 완전히 억제하는 옵션도 제공했습니다.

4.6 Cell Arrays

1990년대 중반, MATLAB 사용자들은 숫자 계산을 넘어서 다양한 데이터 구조를 필요로 하게 되었습니다. 직사각형 형태의 동질적인 숫자 행렬 이상의 일반적인 데이터 구조가 필요했습니다. Cell 배열은 1996년에 도입되었습니다. Cell 배열은 인덱싱된, 가능한 비동질적인 MATLAB 자료들로 이루어진 컬렉션입니다. 이는 다양한 크기와 유형의 배열, 문자열, 다른 cell 배열 등을 담을 수 있습니다. Cell 배열은 중괄호 ‘{ }’를 사용하여 생성됩니다.

c = {magic(3); uint8(1:10); 'hello world'}
c =
    3×1 cell array
    {3×3 double}
    {1×10 uint8}
    {'hello world'}

Cell 배열은 중괄호와 원형 괄호 모두를 사용하여 인덱싱할 수 있습니다. 중괄호를 사용하면 c{k}는 k번째 cell의 내용을 나타냅니다. 원형 괄호를 사용하면 c(k)는 지정된 cell들을 포함하는 cell 배열입니다. Cell 배열을 메일박스의 모음으로 생각해볼 수 있습니다. 원형 괄호를 사용하면 box(k)는 k번째 메일박스를 의미합니다. 중괄호를 사용하면 box{k}는 k번째 상자 안의 편지를 의미합니다.

M = c{1}
c2 = c(1)
M =
    8 1 6
    3 5 7
    4 9 2
c2 =
    1×1 cell array
    {3×3 double}

4.7 구조체

C나 Pascal에서 볼 수 있는 구조체와 연결된 “점 표기법”은 1996년에 도입되었습니다. 현재 그래픽 시스템에서도 이 표기법을 사용합니다. 다른 예로, 작은 반 학생들의 성적표를 만들어 보겠습니다.

Math101.name = {'Alice Jones'; 'Bob Smith'; 'Charlie Brown'};
Math101.grade = {'A-'; 'B+'; 'C'};
Math101.year = [4; 2; 3]

Math101 =
    struct with fields:
    name: {3×1 cell}
    grade: {3×1 cell}
    year: [3×1 double]

출석부를 부르기 위해서는 이름 목록이 필요합니다.

disp(Math101.name)
    'Alice Jones'
    'Bob Smith'
    'Charlie Brown'

Charlie의 학점을 ‘W’로 변경하려면 구조체와 배열 표기법을 함께 사용해야 합니다.

Math101.grade(3) = {'W'};
disp(Math101.grade)
    'A-'
    'B+'
    'W'

4.8 수치적 방법

Forsythe, Malcolm, and Moler의 교과서 [Forsythe et al. 1977]에는 보간, 영점 및 최소값 찾기, 적분, 난수 생성 등과 같은 일반적인 수치적 방법에 대한 Fortran 프로그램이 포함되어 있습니다. 이러한 프로그램을 MATLAB로 번역함으로써 수치적 방법 라이브러리의 시작점이 제공되었습니다.

4.9 상미분방정식(ODE)

상미분방정식의 수치적 해법은 첫 번째 MathWorks MATLAB 이후로 MATLAB의 중요한 부분이었습니다. [Shampine and Reichelt 1997]. ODE(상미분방정식)는 MATLAB의 동반 제품인 Simulink®의 핵심입니다.

Van der Pol 진동자는 고전적인 ODE 예시입니다.

\[\frac{d^2y}{dx^2}=\mu(1-y^2)\frac{dy}{dt}-y\]

매개변수 $\mu$는 감쇠항의 강도를 나타냅니다. $\mu = 0$일 때, 진동자는 고조파 진동 결과를 보여줍니다.

다음 MATLAB 함수는 이 진동자를 1차 방정식의 쌍으로 나타냅니다.

function dydx = vanderpol(t,y)
    mu = 5;
    dydx = [y(2); mu*(1-y(1)^2)*y(2)-y(1)];
end

다음 코드에서는 이 함수의 이름을 포함하는 문자열을 수치적 ODE 솔버 ode23s의 첫 번째 인자로 전달합니다. 이 코드는 Figure 16에 표시된 그래프를 생성합니다.

tspan = [0 30];
y0 = [0 0.01]';
[t,y] = ode23s('vanderpol',tspan,y0);
plot(t,y(:,1),'ko-',t,y(:,2),'k-')
xlabel('t')

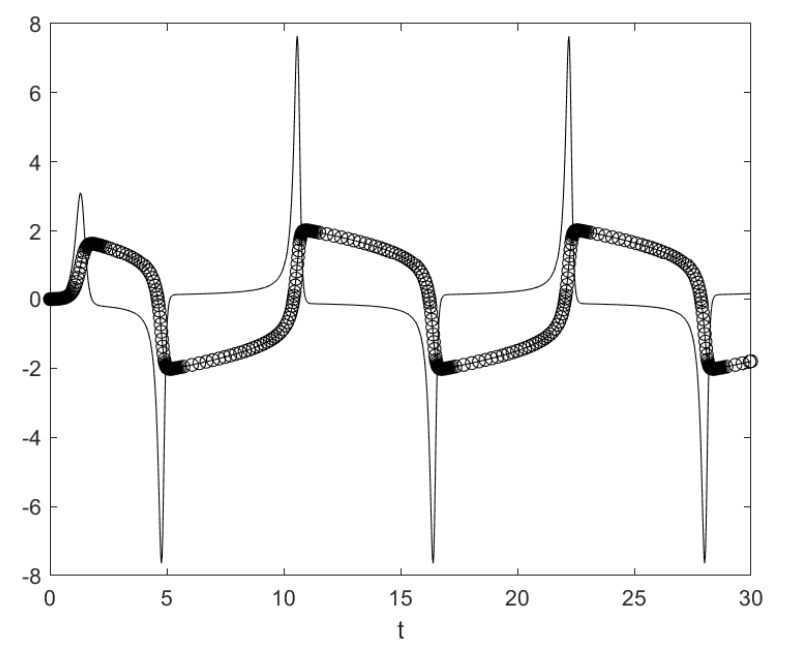
그림 16. Van der Pol 진동자는 고전적인 ODE 예시입니다.

Van der Pol 진동자는 매개변수 $\mu$를 5로 설정한 경우, 약간 강건한(stiff) 미분방정식입니다. 이 코드는 ode23s 솔버를 사용합니다. 여기서 이름에 ‘s’가 포함된 것은 강건한(stiff) 방정식을 위한 것을 의미합니다. 그래프에서 솔루션이 빠르게 변하는 지점들이 몇 군데 집중되어 있는 것을 볼 수 있습니다. 비강건한(nonstiff) 솔버는 훨씬 더 많은 스텝을 취했을 것입니다.

강건한 ODE 솔버는 각 스텝에서 동시 선형 방정식을 풀어야 하는 암묵적 방법을 사용합니다. MATLAB의 유명한 역슬래시(Backslash) 연산자의 구성 요소들이 여기서 조용히 작동합니다.

총 7개의 루틴이 MATLAB ODE 스위트에 있습니다. [na Moler 2014f] 그들의 이름은 모두 “ode”로 시작하며, 그 뒤에 두 자리나 세 자리 숫자가 따르고, 그 뒤에 한 자리 또는 두 자리 문자가 따를 수도 있습니다. 숫자는 방정식의 차수를 나타냅니다. 대략적으로 말하면, 더 높은 차수의 루틴은 더 높은 정확도를 달성하기 위해 더 많은 노력을 기울입니다. 접미사 ‘s’ 또는 ‘t’ 또는 ‘tb’는 강건한(stiff) 방정식을 위한 방법을 나타냅니다. 다음은 이 스위트에 있는 함수 목록입니다.

ode45: 대부분의 비강건(nonstiff) 문제에 대한 첫 번째 선택
ode23: ode45보다 덜 엄격한 정확도 요구사항
ode113: ode45보다 더 엄격한 정확도 요구사항
ode15s: 대부분의 강건(stiff) 문제에 대한 첫 번째 선택
ode23s: ode15s보다 덜 엄격한 정확도 요구사항
ode23t: 수치적 감쇠가 없는 적당히 강건한(stiff) 문제
ode23tb: ode15s보다 덜 엄격한 정확도를 요구함

ode23와 ode45 함수는 비강성(nonstiff) 상미분 방정식을 푸는 데 주요한 MATLAB(및 Simulink) 도구입니다. 두 함수는 모두 단일 단계 ODE(상미분 방정식) 솔버로서, 룬게-쿠타(Runge-Kutta) 방법으로도 알려져 있습니다. 각 단계는 이전 단계와 거의 독립적이지만, 두 가지 중요한 정보가 한 단계에서 다음 단계로 전달됩니다. 원하는 정확도를 달성하기 위해 필요한 단계 크기가 단계별로 전달됩니다. 또한, 성공적인 단계의 끝에서 최종 함수 값이 다음 단계의 초기 함수 값으로 사용되는 FSAL(First Same As Last) 전략이 적용됩니다.

ode23에서 사용되는 BS23 알고리즘은 Larry Shampine과 Przemyslaw Bogacki에 의해 개발되었습니다. 이름에 있는 “23”은 두 개의 동시 단계별 공식(2차 및 3차 순서)이 관련되어 있다는 것을 나타냅니다. 이 두 공식의 차이는 필요에 따라 단계 크기를 조정하는 오차 추정을 제공합니다.

오늘날의 ode45 이전에는 또 다른 버전이 존재했습니다. 1969년에 나온 NASA 보고서에서 Erwin Fehlberg가 “6단계 룬게-쿠타 방법”이라는 이름으로 알려진 방법을 소개했습니다. 이 방법은 단계마다 6개의 함수 평가를 필요로 합니다. 이러한 함수 값은 하나의 계수 집합과 5차 정확도 근사값, 그리고 다른 계수 집합과 독립적인 4차 정확도 근사값으로 결합할 수 있습니다. 이 두 근사값을 비교하여 오차 추정과 결과적인 단계 크기를 제어합니다.

1970년대 초, Shampine과 그의 동료 H. A. (Buddy) Watts는 Sandia Laboratories에서 Fehlberg의 알고리즘을 기반으로 한 Fortran 코드인 RKF45(4차와 5차 근사값을 가지는 룬게-쿠타-펠베르그 방법)를 발행했습니다. 1977년에 Forsythe, Malcolm, 그리고 Moler는 이 RKF45를 그들의 교재인 “수학 계산을 위한 컴퓨터 방법”에서 ODE 솔버로 사용했습니다. RKF45의 Fortran 소스 코드는 현재도 netlib에서 사용 가능합니다. RKF45는 초기 1980년대 MATLAB의 ode45의 기반이 되었으며 초기 버전의 Simulink에도 사용되었습니다. 펠베르그 (4,5) 쌍은 Shampine과 Mark Reichelt가 스위트를 현대화할 때까지 약 15년 동안 사용되었습니다. 오늘날의 ode45 구현은 Dormand와 Prince의 알고리즘을 기반으로 합니다. 이 알고리즘은 6개의 단계를 사용하며, FSAL 전략을 적용하며, 4차 및 5차 공식을 제공하며, 지역 추정과 동반 보간을 포함합니다.

MATLAB 상미분 방정식 스위트의 중심은 ode45입니다. MATLAB 문서에서는 ode45를 첫 번째 선택으로 권장하고, Simulink 블록에서도 ode45를 기본 솔버로 설정합니다. 그러나 ode23은 특정한 단순성을 가지며, 종종 그래픽에 특히 적합합니다. ode23와 ode45를 간단히 비교하면 다음과 같습니다. ode23는 세 단계, 3차 순서의 룬게-쿠타 방법이며, 반면에 ode45는 여섯 단계, 5차 순서의 룬게-쿠타 방법입니다. ode45는 한 단계당 더 많은 작업을 수행하지만 훨씬 더 큰 단계를 취할 수 있습니다.

MATLAB의 상미분 방정식 문법 설계의 중요한 특징은 모든 ODE 솔버를 정확히 동일한 방식으로 사용할 수 있다는 것입니다. 서로 다른 솔버가 인수로 추가 정보가 필요할 수 있지만, 7개의 함수 모두 동일한 API를 갖고 있으므로 적절한 값을 인수로 제공하는 것만으로 해결됩니다(일부 솔버에서는 이러한 값들 중 일부가 무시될 수 있습니다). 특히, 원하는 솔루션 지점(영역 내에서)을 지정하는 유연한 옵션과 필요한 경우 자동으로 보간이 수행되어 이러한 솔루션 지점을 생성할 수 있습니다. 이는 좋은(부드럽게 보이는) 플롯을 생성하는 데 특히 중요할 수 있습니다.

4.10 텍스트

MATLAB은 Unicode 문자 집합을 사용합니다. 문자 벡터는 작은 따옴표로 구분됩니다.

다음 문장을 실행하면

h = 'hello world'

다음과 같은 결과가 나옵니다.

h =
    'hello world'
disp(h)
    'hello world'
d = uint8(h)
d =
    1×11 uint8 row vector
    104 101 108 108 111 32 119 111 114 108 100

짧은 문자열은 종종 함수의 선택적 매개변수로 사용됩니다.

[U,S,V] = svd(A,'econ'); % 경제 사이즈, U는 A와 동일한 모양.
plot(x,y,'o-') % 데이터 포인트에 원과 함께 선 그래프를 그립니다.

여러 줄의 텍스트 또는 단어 배열의 경우, 문자 배열이 직사각형 모양이 되도록 공백으로 채워져야 합니다. char 함수를 사용하여 이를 수행할 수 있습니다. 예를 들어, 다음은 3x7 배열입니다.

class = char('Alice','Bob','Charlie');
class =
    3x7 char array
    'Alice  '
    'Bob    '
    'Charlie'

또는 cell 배열을 사용할 수도 있습니다.

class = {'Alice', 'Bob', 'Charlie'}'
class =
    3x1 cell array
    {'Alice' }
    {'Bob' }
    {'Charlie'}

최근에는 포괄적인 문자열 데이터 유형이 도입되었습니다. (5.10절 참조)

4.11 MathWorks 로고의 진화

MathWorks는 아마도 세계에서 유일하게 로고로 편미분 방정식의 해를 가지고 있는 회사입니다. 그래픽은 시간이 지남에 따라 진화했습니다 [na Moler 2014c; na Moler 2014e; na Moler 2014d; na Moler 2014b; na Moler 2014a]. 초기에는 2차원 등고선 플롯이었으며, Cleve Moler의 박사 학위 논문 [Moler 1965, Figure (8.15)]에 해당 버전의 플롯이 나왔습니다. 이후 3차원 흑백 표면 플롯으로 진화하고, 다양한 색상과 조명 모델을 적용한 3차원 플롯으로 발전했습니다 (그림 17 참조).

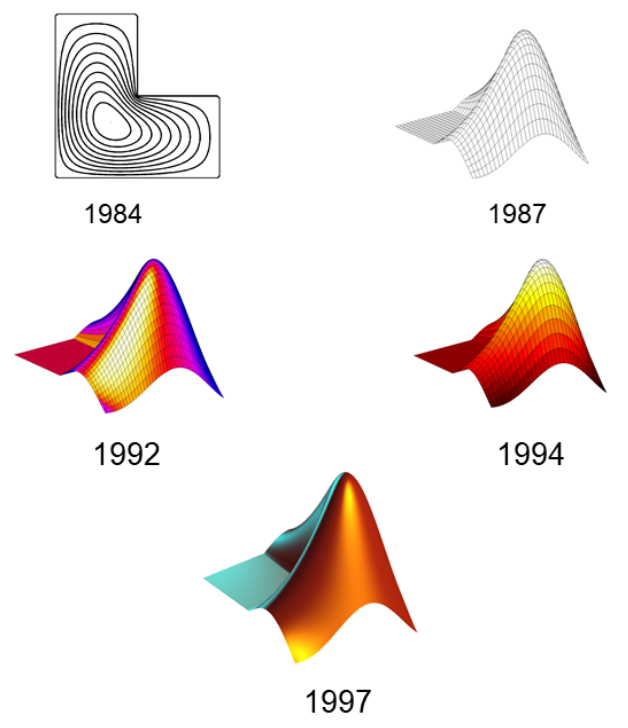
그림 17. MathWorks 로고의 진화: 2차원 등고선 플롯에서 3차원 표면 플롯으로 색상과 조명이 적용된 형태로 진화하였습니다. (출처: MathWorks.)

5 최근 개발 동향

5.1 LAPACK

2000년, MathWorks는 수치 선형 대수 라이브러리로 Fortran 세계로 돌아와서 MATLAB 6에서 LAPACK [Anderson et al. 1999]을 도입하였습니다. 이로 인해 이전에 C로 재작성된 LINPACK 및 EISPACK 서브루틴 컬렉션을 대체하였습니다. 다음은 이 큰 전환에 대한 일부 코멘트입니다 [na Moler 2000]:

MATLAB은 1970년대 후반에 상태가 최신인 행렬 계산용 Fortran 서브루틴 라이브러리인 LINPACK과 EISPACK을 기반으로 한 대화식 계산기로 시작되었습니다. MATLAB의 모든 버전에 대한 수학적 핵심은 버전 5.3까지 LINPACK과 EISPACK의 약 12개 정도의 Fortran 서브루틴들의 C로의 번역을 사용해왔습니다. LAPACK은 LINPACK과 EISPACK의 현대적인 대체재입니다. 이는 대규모, 다중 저자의 수치 선형 대수를 위한 Fortran 라이브러리입니다. 7월에 새로운 버전이 출시되어 NETLIB (www.netlib.org/lapack)에서 이용 가능합니다. LAPACK은 원래 초고속 컴퓨터 및 기타 고급 기기에서 사용하기 위해 고안되었습니다. 이는 블록 알고리즘을 사용하며, 한 번에 여러 열의 행렬에 작용합니다. 고속 캐시 메모리를 갖춘 기기에서는 이러한 블록 연산이 상당한 속도 이점을 제공할 수 있습니다. LAPACK은 이전 버전보다 더 다양한 기능 세트를 제공합니다.

모든 이러한 패키지의 속도는 기본 선형 대수 서브루틴(BLAS)의 속도와 밀접하게 관련됩니다. EISPACK은 BLAS를 사용하지 않았습니다. LINPACK은 Level 1 BLAS를 사용했으며, 이는 한 번에 하나 또는 두 개의 벡터 또는 행렬의 열에 작용합니다. 지금까지 MATLAB은 이러한 Level 1 BLAS의 신중하게 작성된 C 및 어셈블리 언어 버전을 사용해왔습니다. LAPACK의 블록 알고리즘은 또한 Level 2와 Level 3 BLAS를 활용하여 전체 행렬의 큰 부분에 작용합니다. LAPACK의 NETLIB 배포판에는 Fortran으로 작성된 Reference BLAS가 포함되어 있습니다. 그러나 저자들은 각 하드웨어와 운영 체제 제조업체가 해당 시스템에 최적화된 BLAS의 다양한 버전을 제공할 것으로 의도하였습니다.

마침내 LAPACK을 MATLAB에 통합할 시기가 왔습니다. 거의 모든 최신 기기에서는 LAPACK의 설계로부터 이점을 얻을 수 있습니다. 몇몇 핵심 칩 및 컴퓨터 공급업체는 최적화된 Level 1, 2, 3 BLAS를 제공합니다. University of Tennessee의 연구 프로젝트인 ATLAS에서는 특정 기기에 최적화된 루틴을 매개변수화된 코드 조각에서 자동으로 생성할 수 있는 새로운 대체재가 제공됩니다.

MATLAB의 초기 버전은 첫 번째 PC에서 사용 가능한 반 메가바이트의 메모리에서 실행되었기 때문에 코드 크기를 최소화하는 것이 필요했습니다. 복소 및 일반화된 고유값 문제를 위해 LINPACK이나 EISPACK에 없는 단일 변위 복소 QZ 알고리즘을 하나의 일반적인 고유값 루틴으로 개발하였습니다. 현재 LAPACK에서 제공되는 다양한 함수 목록으로 인해 MATLAB의 공간 절약 일반용 코드는 더 빠르고 중점적인 루틴으로 대체될 수 있습니다. eig 함수에는 이제 한 개 또는 두 개의 인수가 있는지, 인수가 실수인지 복소수인지, 문제가 대칭인지, 그리고 고유벡터가 요청되는지에 따라 16개의 다른 코드 경로가 있습니다.

… 유감스럽게도 LAPACK 도입과 함께 인기 있는 MATLAB 기능 중 하나가 희생되어야 합니다. 연산 횟수를 계산하는 flops 함수는 더 이상 실행 가능하지 않습니다. 대부분의 부동 소수점 연산은 이제 flop 카운트를 유지하지 않는 최적화된 BLAS에서 이루어지기 때문입니다. 하지만 현대의 컴퓨터 구조에서는 부동 소수점 연산이 더 이상 실행 속도의 주요 요소가 아닙니다. 메모리 참조와 캐시 사용이 가장 중요합니다.

5.2 FFTW

MATLAB 5.3과 266 MHz 펜티엄 노트북을 사용하여 백만 점의 실수 FFT는 약 6초가 걸렸습니다. 2000년에는 MATLAB 6.0에 새로운 FFT 코드가 통합되면서 동일한 계산에 약 1.2초가 걸렸습니다. 이 새로운 코드는 Matteo Frigo와 Steven G. Johnson이 매사추세츠 공과대학교에서 개발한 “서쪽에서 가장 빠른 푸리에 변환(FFTW)”에 기반합니다 [Frigo 1999; Frigo and Johnson 1998]. Frigo와 Johnson은 이 작업으로 1999년 J. H. Wilkinson 수치 소프트웨어 상을 수상하였습니다.

MATLAB 5의 fft 함수는 길이가 작은 소수의 곱인 경우에만 빠른 FFT 버전을 사용할 수 있었고, 그렇지 않으면 느린 FFT(길이에 비례하여 제곱 시간이 소요되는)를 사용해야 했습니다. FFTW의 개선으로 MATLAB 6은 어떤 길이든 빠른 FFT 알고리즘을 사용할 수 있게 되었습니다, 심지어 큰 소수인 경우에도 가능합니다.

측정 결과, 길이 𝑛이 2의 거듭제곱이며 216 = 65536 이하인 경우, MATLAB 5.3과 MATLAB 6.0의 fft 실행 시간은 거의 동일했습니다. 하지만 𝑛이 2의 거듭제곱이고 216보다 큰 경우, MATLAB 6.0은 캐시 메모리를 더 효과적으로 사용하여 약 두 배 빨랐습니다. 𝑛이 소수이고 2의 거듭제곱이 아닌 경우, MATLAB 6.0은 MATLAB 5.3보다 두 배에서 네 배 정도 더 빨랐습니다. [na Moler and Eddins 2001]

5.3 데스크탑

MATLAB 데스크탑은 2000년에 도입되었습니다 [na Moler 2018f]. 그림 18은 오늘날 데스크탑의 기본 레이아웃을 보여줍니다. 왼쪽에는 현재 폴더 뷰어, 오른쪽에는 워크스페이스 뷰어, 상단 가운데에는 편집기/디버거, 하단 가운데에는 기존의 명령 창이 표시됩니다. 파일 뷰어와 명령 기록 창은 기본 레이아웃에 포함되어 있지 않지만 사용자 정의 레이아웃에 포함시킬 수 있습니다.

패널 중 하나는 닫거나 독립적인 창으로 만들 수 있습니다. 두 개의 화면을 사용할 수 있는 경우, 하나의 화면에 명령 창을 두고 다른 화면에 편집기를 놓을 수 있습니다.

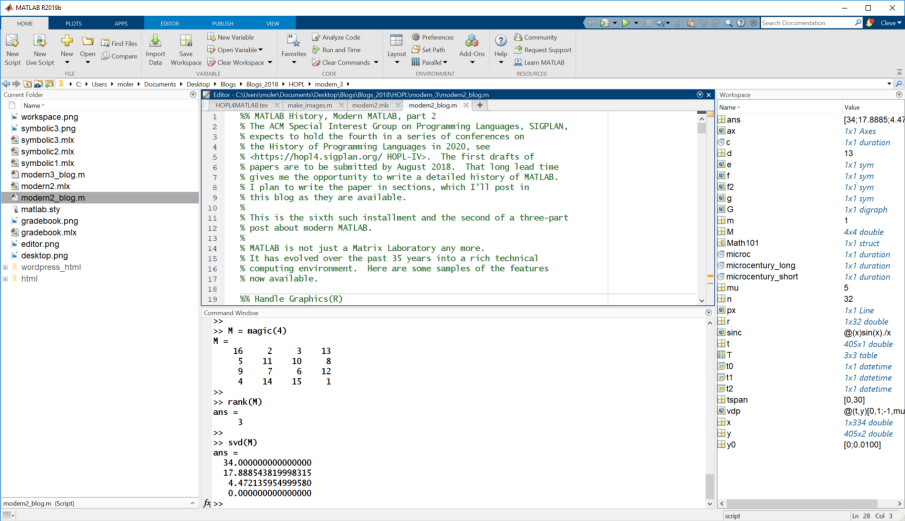
그림 18. MATLAB 데스크탑의 모습 (2019년)

5.4 함수 핸들

MATLAB에는 다른 함수를 인수로 받는 여러 함수들이 있습니다. 이러한 함수를 “함수 함수”라고 합니다. 오랫동안 함수 인수는 문자열로 지정되었습니다. Van der Pol 진동자의 수치적인 해법은 앞에서 언급한 예제입니다. 함수 vanderpol.m은 2x1 차원 1계 미분 방정식을 정의합니다.

function dydt = vanderpol(t,y)
dydt = [y(2); 5*(1-y(1)^2)*y(2)-y(1)];
end

그런 다음 함수 이름은 문자열로 ODE solver ode45에 전달됩니다.

tspan = [0 150];
y0 = [1 0]';
[t,y] = ode45('vanderpol',tspan,y0);

결과적으로 이 계산에 필요한 시간의 절반 이상이 문자열 인수를 반복적으로 디코딩하는 데 소요됩니다. 성능은 함수 핸들의 도입으로 개선되었습니다. 함수 핸들은 “@”(at sign)으로 시작하는 함수 이름을 사용합니다.

또한 “@”(at sign)은 익명 함수를 정의하는 함수 핸들을 생성하는 데 사용되며, 이는 Church의 람다 계산의 MATLAB 인스턴스입니다. 유례적으로 익명 함수는 종종 실제로 변수에 할당되어 익명성이 상쇄됩니다.

vdp = @(t,y) [y(2); 5*(1-y(1)^2)*y(2)-y(1)];

Van der Pol 통합에서 문자열, 함수 핸들 및 익명 함수를 사용하여 소요된 시간을 비교해 봅시다.

tic, [t,y] = ode45('vanderpol',tspan,y0); toc
Elapsed time is 0.200928 seconds.
tic, [t,y] = ode45(@vanderpol,tspan,y0); toc
Elapsed time is 0.076443 seconds.
tic, [t,y] = ode45(vdp,tspan,y0); toc
Elapsed time is 0.051992 seconds.

후자 두 개의 소요 시간은 비교 가능하며 첫 번째 것보다 훨씬 빠릅니다. 익명 함수는 다른 익명 함수의 값으로 반환될 수 있으며, 오늘날 흔히 “렉시컬 스코핑(lexical scoping)”이라고 불리는 것이 적절하게 관찰되어 안쪽 함수가 바깥쪽 함수에 의해 바인딩된 변수를 참조할 수 있습니다. 그러나 MATLAB 문법은 함수를 계산하고 즉시 인수에 적용하는 방법을 제공하지 않으므로 다음과 같은 표현은 (LISP 프로그래머가 MATLAB에서 기대하는 것처럼) 구문 오류로 거부됩니다.

((@(x)(@(y)x+y))(3))(5)

그러나 함수 핸들이 변수에 할당되는 경우:

fx = @(x)(@(y)x+y); 
fy = fx(3); 
fy(5)

예상한 답인 8이 실제로 생성됩니다. fy의 함수 핸들은 변수 x가 값 3을 가졌음을 “기억”합니다.

또 다른 방법은 feval 함수(함수 평가를 위한)를 사용하는 것입니다.

fx = @(x)(@(y)x+y);
feval(feval(fx,3),5)

5.5 객체

MATLAB 사용자는 다양한 프로그래밍 기술을 갖춘 사람들로 이뤄져 있습니다. 스펙트럼의 한쪽 끝에는 일반적인 프로그래밍에는 관심이 적지만 기술적인 계산에는 MATLAB을 광범위하게 사용하는 과학자와 엔지니어들이 있습니다. 그들에게는 프로그래밍의 용이성이 주요하다고 할 수 있습니다. 다른 한편으로는 MathWorks에서 일하는 프로페셔널 프로그래머들을 포함한 사람들이 있습니다. 이들은 풍부하고 강력한 프로그래밍 언어를 원합니다.

주로 내부 요구에 응답하여, 2008년에는 C++과 Java에서 찾을 수 있는 기능을 갖춘 MATLAB 객체 지향 프로그래밍 능력에 큰 개선이 이루어졌습니다. 클래스를 생성함으로써 특수화된 데이터 구조나 많은 함수를 포함하는 프로그래밍 작업을 단순화할 수 있습니다. MATLAB 클래스는 함수와 연산자 오버로딩, 속성과 메서드의 제어된 접근, 참조와 값의 의미론, 이벤트와 리스너를 지원합니다. MATLAB 그래픽 시스템은 객체 지향 접근법의 크고 복잡한 예입니다.

5.6 Symbolic Math Toolbox™

수학적으로, MATLAB은 종종 MACSYMA [Martin and Fateman 1971] 및 그 계열과 비교됩니다. 이러한 symbolic algebra 시스템의 주요 데이터 구조는 어떤 형태의 기호식입니다. 가장 기본적인 수준에서 이러한 시스템은 미적분을 수행할 수 있습니다. 예를 들어, 이들은 cos𝑥의 도함수가 -sin𝑥임을 알고 있습니다. 숫자 계산도 가능하지만 이는 이들의 강점은 아닙니다.

MATLAB에서 기호적 조작은 선택적으로 추가되는 Symbolic Math Toolbox로 수행됩니다. 이 툴박스는 현재 버전 8.4에 해당합니다. 다음 명령은 sym 메서드를 사용하는 400개 이상의 함수를 나열합니다.

methods sym

이 툴박스는 기호적 수학 방정식을 풀고, 그래프를 그리고, 조작하는 데 필요한 함수들을 제공합니다. 이러한 작업에는 미분, 적분, 단순화, 변환 및 방정식 해결이 포함됩니다. 연산은 분석적으로 또는 변수 정밀도 산술을 사용하여 수행될 수 있습니다.

5.7 MATLAB을 더 접근 가능하게 만들기

최초 버전의 MATLAB은 간단한 터미널 응용 프로그램이었습니다. 시간이 지나면서 그래픽, 편집 및 기타 도구를 위한 별도의 창이 추가되었습니다. 이러한 변경으로 MATLAB은 사용하기 쉬워지며 특히 이전 프로그래밍 경험이 없는 사용자들에게 유용해졌습니다. 가장 큰 영향을 미친 두 가지 기능은 위에서 설명한 MATLAB 데스크톱과 라이브 에디터입니다.

2016년에 도입된 MATLAB 라이브 에디터 노트북 인터페이스는 MATLAB의 입력, 출력 및 그래픽을 하나의 대화식 문서로 결합합니다. 이 문서는 HTML, PDF 또는 LATEX로 내보낼 수 있습니다.

Figure 19-21은 라이브 에디터가 Symbolic Math Toolbox 결과를 조판하는 확장된 예제를 보여줍니다.

그림 19. MATLAB 라이브 에디터에서 Symbolic Math Toolbox를 사용하는 예시 (1/3)

그림 20. MATLAB 라이브 에디터에서 Symbolic Math Toolbox를 사용하는 예시 (2/3)

그림 21. MATLAB 라이브 에디터에서 Symbolic Math Toolbox를 사용하는 예시 (3/3)

오락적인 수학에서 나온 “매직 스퀘어”는 (모든 열, 행 및 두 대각선이 같은 합을 갖는 1부터 𝑛2까지의 정수를 포함하는 𝑛-𝑛 매트릭스)는 선형 대수학적인 관점에서 흥미로운 특성을 갖습니다. 이것이 바로 초기 MATLAB 디자인에 매직 스퀘어를 생성하는 함수가 포함된 이유입니다. 초기 문서에서는 함수 magic이 “흥미로운 테스트 매트릭스”를 생성한다고만 언급되었습니다 [Moler 1980]. 1981년 매뉴얼에는 “매직 스퀘어. MAGIC(N)은 N x N 행렬로, 정수 1부터 N**2까지를 사용하여 행과 열의 합이 같도록 만들어집니다.”라고 설명되어 있습니다.

Figure 22와 23은 Classic MATLAB을 사용하여 4x4 매직 스퀘어의 여러 속성을 보여주는 데모를 보여줍니다. 이에는 모든 행, 열 및 주 대각선의 합이 34인 사실과 랭크가 3이 아닌 4인 특성이 포함됩니다. Figure 24와 25는 오늘날의 MATLAB Live Editor™를 사용하여 비슷한 데모를 보여줍니다.

그림 22. Classic MATLAB에서 매직 스퀘어의 간단한 특성들을 파악하는 예시 (1/2)

그림 22. Classic MATLAB에서 매직 스퀘어의 간단한 특성들을 파악하는 예시 (2/2)

5.8 병렬 컴퓨팅

Parallel Computing Toolbox™(PCT)는 2004년 슈퍼컴퓨팅 컨퍼런스에서 처음으로 소개되었습니다. 그 다음 해인 2005년 슈퍼컴퓨팅 컨퍼런스에서는 빌 게이츠가 키노트 강연을 하며, MATLAB을 사용하여 마이크로소프트의 고성능 컴퓨팅 분야 진출을 시연했습니다.

PCT는 거친 단위의 분산 메모리 병렬 처리를 지원하여 여러 대의 컴퓨터나 단일 기계의 많은 코어에서 많은 MATLAB 워커를 실행합니다. [Luszczek 2009]

PCT의 가장 인기 있는 기능은 parallel for loop 명령어인 parfor입니다. 이를 통해 단일 프로그램의 다양한 변형들을 생성하고 프로세스 간 통신이 없는 “처치 곤란 병렬(embarrassingly parallel)” 작업을 수행할 수 있습니다.

Parallel Computing Toolbox는 MPI (Message Passing Interface) 라이브러리 [Gropp 등, 1998; Snir 등, 1998] 구현을 기반으로 합니다. MATLAB은 MPI 표준에서 정의된 함수들의 고수준 추상화인 메시지 패싱 함수를 제공합니다. 이에는 점대점 통신, 브로드캐스트, 배리어, 그리고 축소 작업 등이 포함됩니다. Parallel Computing Toolbox의 중요한 설계 요소 중 하나는 메시지를 이용하여 임의의 MATLAB 데이터 타입을 전송하거나 교환할 수 있다는 점입니다. 이에는 임의 정밀도의 숫자 배열, 구조 배열, 그리고 셀 배열 등이 포함됩니다.

일반적인 경우, 하나의 MATLAB 메시지는 두 개의 MPI 메시지가 됩니다. 첫 번째 메시지는 알려진 크기의 짧은 헤더 메시지로, MATLAB 데이터 타입과 관련된 크기 정보를 나타냅니다. 그 후에는 페이로드 메시지가 이어지게 됩니다. 첫 번째 메시지의 크기 정보를 이용하여 수신자는 페이로드를 수용할 충분한 버퍼를 준비할 수 있습니다. 특정 작은 데이터 크기의 경우, 페이로드는 헤더 메시지에 포함되어 별도의 페이로드 메시지가 필요하지 않게 됩니다. 복잡한 데이터 타입의 경우, 데이터 배열은 발신자에 의해 바이트 스트림으로 직렬화되고, 이후에 수신자에 의해 역직렬화됩니다. 그러나 MPI 데이터 타입으로 직접 매핑될 수 있는 MATLAB 데이터 타입의 경우, 직렬화/역직렬화 과정이 생략되고 데이터 배열의 내용이 직접 전송됩니다. [Sharma와 Martin, 2009]

5.9 그래픽 처리 장치(GPU)

그래픽 처리 장치(GPU) 지원이 2010년에 Parallel Computing Toolbox에 추가되었습니다. 8년 뒤인 릴리스 R2018a에서, gpuarray는 lu, eig, svd 및 mldivide (역슬래시 연산자)를 포함한 모든 익숙한 행렬 계산을 포함한 385개의 관련 메서드가 있는 상태로 성장했습니다.

5.10 문자열

2016년에 MathWorks는 더 포괄적인 텍스트 지원을 제공하기 위해 쌍따옴표 문자와 문자열 배열 데이터 구조를 도입하기 시작했습니다. 다음 문장은 다음과 같이 작동합니다.

class = ["Alice", "Bob", "Charlie"]'

결과:

class =
3×1 string array
"Alice"
"Bob"
"Charlie"

새로운 문자열 데이터 타입을 위한 매우 편리한 함수들이 있습니다.

proverb = "A rolling stone gathers momentum"
words = split(proverb)

결과:

proverb =
"A rolling stone gathers momentum"
words =
5×1 string array
"A"
"rolling"
"stone"
"gathers"
"momentum"

문자열의 덧셈은 연결(concatenation)입니다.

and = " and ";
merge = class(1);
for k = 2:length(class)
    merge = merge + and + class(k);
end
merge

결과:

merge =
"Alice and Bob and Charlie"

regexp 함수는 Unix 및 다른 많은 프로그래밍 언어에서 볼 수 있는 정규 표현식 패턴 매칭을 제공합니다.

5.11 실행 엔진

최근 몇 년 동안, MATLAB 코드의 실행 방식에 변화가 있으며 이에 따른 성능 향상도 이루어졌습니다. 이러한 변화는 MATLAB 코드를 기계 코드로 JIT(just-in-time) 컴파일하는 것에 기반을 두고 있습니다.

첫 번째 MATLAB JIT 컴파일러는 2000년대 초에 도입되었으며, 완전한 함수를 한 번에 컴파일했지만 엄격한 제약 조건이 충족되었을 때에만 그리고 MATLAB 언어의 일부에 대해서만 컴파일되었습니다. 따라서 이 첫 번째 JIT 컴파일러는 전체적인 MATLAB 성능에 상대적으로 작은 영향을 미쳤습니다. 2015년에 추적(trace)-기반 JIT 컴파일러가 도입되었습니다. 이 컴파일러는 원래의 인터프리터를 완전히 대체하였습니다. 이는 추적 또는 특정 코드 경로를 실행 시간에 프로그램 변수의 동적 유형을 알고 컴파일하는 것을 기반으로 합니다. 이 새로운 MATLAB 실행 엔진은 재사용을 위해 컴파일된 추적을 캐시하고 이들 사이에 빠른 조회 링크를 기록합니다.

이 새로운 JIT 컴파일러는 진화를 염두에 두고 구축되었습니다. 다양한 종류의 코드를 지원하기 위해 컴파일 및 최적화의 여러 레이어가 만들어졌습니다: • 긴 직선형 코드 스크립트. 이들은 종종 세션 당 한 번 또는 몇 번만 실행되므로 실행 시간 절감으로 컴파일 비용이 상환되지 않습니다. • 단순한 행렬 인덱싱 및 산술 연산을 포함하는 조밀한 루프를 가진 포트란과 유사한 코드. • 벡터화된 코드, 복잡한 배열 인덱싱 및 다양한 특수 함수 호출을 포함하는 라이브러리 풍 테크니컬 컴퓨팅.

이제 JIT 컴파일러는 경량 분석 및 컴파일 전략을 사용하여 긴 코드 스크립트를 빠르게 실행할 수 있습니다. 루프 경계를 넘어서 추적을 연결하고, 포트란과 유사한 코드에 대한 다양한 루프 최적화를 가능하게 합니다. 그리고 가장 복잡하고 풍부한 코드의 경우, CPU 코어 및 백그라운드 스레드를 여러 개 사용하여 분석이 완료될 때까지 코드 실행을 기다릴 필요가 없도록 깊은 분석 및 최적화를 수행할 수 있습니다. 전형적인 MATLAB 워크플로우는 이제 코드 변경이 필요하지 않고, 평균적으로 4년 전보다 두 배 빠르게 실행됩니다.

이 다층 JIT 컴파일 전략은 현재 MathWorks에서 개발 중인 분야 중 하나입니다.

5.12 개발 과정

MathWorks 초기에는 몇 사람만이 MATLAB 소스 코드에 작업을 진행했습니다. 원칙적으로 누구든지 코드의 어떤 부분이든 변경할 수 있었습니다. 하지만 실제로는 사람들이 각자의 전문분야에만 집중했습니다.

오늘날 개발 과정은 훨씬 더 체계적이고 전문적입니다. 어떤 변경 또는 추가 사항에 대한 공식적인 제안은 위원회에서 검토됩니다. 동료 코드 리뷰가 필요합니다. 변경 사항이 수락되기 전에 광범위한 자동화된 테스트가 수행됩니다.

개발 프로세스는 두 가지 강력한 사내 시스템을 통해 이루어집니다. 버그 추적 시스템은 “Gecko”라는 이름의 시스템입니다. 이는 버그를 먹는 도마뱀에서 따온 이름입니다. Gecko는 소프트웨어에 영향을 미치는 거의 모든 활동을 추적하는 시스템으로 진화했습니다. 테스트 시스템은 “Build and Test” 또는 “BaT”입니다. 각 개발자는 “샌드박스”에 개인용 MATLAB 사본과 함께 작업 중인 소프트웨어를 가지고 있습니다. 어떤 종류의 변경 사항이든 개인 샌드박스에서 수행할 수 있습니다. MATLAB의 일부가 되기 위해서는 BAT에 작업이 제출되어야 합니다. 다음 릴리스에 허용되기 전에 다단계 테스트 스위트를 통과해야 합니다.

MathWorks는 “연속적 통합(continuous integration)”의 선구자 중 하나였으며, 이 용어가 널리 사용되기 전에도 이미 이를 도입했습니다. MATLAB 4.0은 모든 플랫폼에 대해 포팅하고 릴리스하는 데 거의 2년이 걸렸습니다. 새로운 다중 플랫폼 연속 통합 시스템을 통해 MATLAB 5.0은 PC, Mac 및 여러 Unix 플랫폼에 동시에 릴리스되었습니다. 전체 제품 스위트는 매년 두 번씩 릴리스됩니다. 일부 큰 조직은 1년에 두 번 이상 릴리스를 설치하기보다는 덜 자주 릴리스를 선택할 수 있습니다.

5.13 툴박스

오늘날 MATLAB의 많은 기능은 특화된 응용 분야에 제공되는 툴박스에서 나옵니다. 릴리스 2018a에서는 총 63개의 툴박스가 있습니다. 다음은 각 범주입니다.

병렬 컴퓨팅 (2)
수학, 통계 및 최적화 (9)
제어 시스템 (8)
신호 처리 및 무선 통신 (11)
이미지 처리 및 컴퓨터 비전 (6)
테스트 및 측정 (5)
계산 금융 (8)
계산 생물학 (2)
코드 생성 (7)
응용 프로그램 배포 (3)
데이터베이스 접근 및 보고 (2)

5.14 오늘날의 why 명령어

클래식 MATLAB의 why 명령어는 소프트웨어 리팩터링, 업그레이드 및 릴리스를 넘어서 40년 이상의 세월을 이겨내며 여전히 인기를 끌고 있습니다. 10개의 고정된 응답 외에도, 이제 명사, 동사, 형용사 및 부사를 포함한 문법적으로 올바른 영어 문장을 무작위로 생성할 수 있습니다. 가능한 예시:

why

Some old and nearly bald mathematician suggested it.

6. 성공

MathWorks는 현재 5000명 이상의 직원을 고용하고 있으며(그 중 30%는 미국 외부에 위치), 2018년에는 10억 달러 이상의 수익을 올렸으며(이 중 60%는 미국 외부에서 발생), 185개 국가의 고객 및 10만 개 이상의 비즈니스, 정부 및 대학 사이트에 소프트웨어가 설치되어 있습니다 [na MathWorks, Inc. 2019]. 전 세계적으로 6,500개 이상의 대학과 대학교가 다양한 기술 분야의 교육 및 연구에 MATLAB과 Simulink를 사용하고 있습니다. 전 세계에서 MATLAB를 사용하는 사용자는 4백만 명을 넘고, 27개 언어로 된 2000개 이상의 MATLAB 기반 서적이 있습니다.

MATLAB의 성공의 이유는 무엇일까요? 여러 가지 이유가 있습니다.

수학. 몇 년 전 조지아 공과대학의 Jim McClellan 교수가 “MATLAB가 신호 처리에 대해 매우 우수한 이유는 신호 처리를 위해 설계되지 않았기 때문입니다. 수학을 수행하기 위해 설계되었습니다.”라고 말했습니다. 이와 마찬가지로 신호 처리 외에도 수많은 분야에서 동일한 말을 할 수 있습니다. 행렬과 상미분 방정식은 오늘날 기술적인 컴퓨팅의 기초입니다.

품질. MATLAB 결과는 그 정밀성과 정확성으로 알려져 있습니다.

언어. 근본적으로 MATLAB는 배열을 조작하기 위한 컴퓨터 프로그래밍 언어입니다. 배열 연산, 첨자 표기법 및 for 루프의 간결함과 강력함은 수치 선형 대수를 넘어서서 유용하게 사용되었습니다.

툴박스. MATLAB가 선형 대수와 수학에 대해 수행한 것처럼 다양한 특화된 라이브러리는 MATLAB를 확장하여 수학적 알고리즘에 의존하는 학문 분야에서 기본 도구를 제공합니다. 특히 선형 대수 또는 배열 기반의 경우 이는 신호 처리, 제어 시스템, 이미지 처리, 통계, 최적화 및 기계 학습과 같은 영역을 포함합니다.

그래픽. 많은 사람들은 MATLAB을 그래픽 작업만을 위해 사용합니다. 선 그래프, 막대 그래프, 산점도, 파이 차트, 3차원 그래프, 동영상 등 - 목록은 매 릴리스마다 확장됩니다. 출판 품질의 그래픽을 생성하는 것은 항상 MATLAB의 강점 중 하나였습니다.

상호 작용성. MATLAB은 원래 학생들에게 Fortran이나 C의 배치 처리 및 편집-컴파일-링크-로드-실행 워크 플로우의 지연 없는 행렬 계산 방법을 제공하는 것을 목표로 하였습니다. 이것은 메인프레임과 타임 쉐어링 시대의 초기에 매력적이었으며, 오늘날에도 각자 개인용 컴퓨터를 가지고 있는 상황에서 여전히 매력적입니다.

교육. 학생들은 대학에서 처음으로 MATLAB을 접하고 졸업 후 산업 현장에서 유용하게 사용합니다.

문서화. 전문적으로 작성되고 면밀하게 유지되며 강력한 문서 정보 구조와 광범위한 사용성 테스트로 백업되는 문서입니다.

지원. MathWorks는 정기적인 반기간 릴리스, 빠른 이메일 및 전화 지원, 온라인 및 내부 교육, 컨설팅 및 강력한 사용자 커뮤니티를 포함한 전문적인 지원을 제공합니다.

웹. mathworks.com 웹 사이트는 처음 등록된 상업용 인터넷 사이트 중 하나였으며, 회사는 웹 사이트를 통해 많은 MATLAB 워크플로우를 제공합니다. 이에는 MATLAB 온라인, 코드 교환, 온라인 교육 및 포괄적인 비디오 “어떻게” 예제가 포함됩니다.

아마도 MATLAB의 인기 성공의 한 가지 추가적인 측정은 최근에 ‘MATLAB for Dummies’이라는 책이 출간된 것입니다 [Sizemore and Mueller 2014].

에필로그

Moler는 처음에 이 모든 것을 동기로 한 행렬 분석 강좌를 가르칠 수 없었습니다. ‘클래식 MATLAB’이 다른 사람들이 사용할 수 있을 정도로 준비될 때, 그는 컴퓨터 과학 부에 있었으며 다른 책임들이 있었습니다.

감사의 말

이 논문에 대한 중요한 개선 사항에 대해 MathWorks의 Steve Eddins와 Jonathan Foot, Guy Steele 및 HOPL 선임 과정에 감사드립니다.

(이하 부록은 생략합니다.)