본 포스팅은 아래의 MathWorks 김종헌 프로님의 Path Planning 시리즈 중 아래의 비디오를 정리한 것입니다.
이 비디오에서는 모바일 패스 플레이닝 시리즈 미디어의 세 번째 파트로 Navigation toolbox에서 제공하는 global path planning algorithm에는 어떤 것들이 있는지 그리고 그 중에서도 오늘 이 시간에는 route planning에 대해서 설명한다.
Types of Path Planning Algorithms

그림 1. 매트랩 Navigation Toolbox에서 제공하는 Global Path Planning 알고리즘의 구분
Navigation Toolbox는 다양한 형태의 global path planning algorithm을 제공하고 있다. 그 알고리즘을 분류를 하면서 설명을 하자면
먼저 path planner가 동작하는 공간의 형태에 따라서 이산 공간/연속 공간으로 나뉘는데 이산 공간에서 가장 간단한 형태의 탐색 기반의 planning approach로 그리드 기반의 A* 알고리즘과 그래프 기반의 A* 알고리즘을 제공하고 있다. 연속 공간에서도 탐색 기반 탐색 기반 planning approach를 제공하는데 자동차와 같은 조향 mechanism을 갖는 로봇을 위한 hybrid A* 알고리즘이 여기에 속한다.
PRM, RRT 그리고 몇가지 변형 RRT 알고리즘을 제공하여 연속 공간을 임의로 sampling하여 planning하는 approach를 지원하고 있다. 그리고 마지막으로 Model predictive control toolbox를 이용해 최적화 기반의 플래닝 어프러치도 지원하고 있다. 이 중에서 오늘은 모든 플래너들을 이해하는데 가장 기본이 되는 path planning이란 이런 것이구나 라는 것을 이해하는 데 가장 기초가 되는 A* 알고리즘에 대해서 알아보자.
A* Algorithm
A* 알고리즘은 목적지에 도달하기 위해 어떤 길이 가장 좋은 길인가를 결정할 때 제일 먼저 떠오르는 알고리즘이다.
여러가지 변형이 존재하지만 가장 기본적인 A* 알고리즘을 기준으로 설명하기 위해 그림 2와 같이 단순한 그리드 위에서 path planning을 실행해보자. Grid는 path planning을 할 공간을 같은 크기의 격자로 이산화 시키고, 이렇게 이산화되어 나타나는 질점 (노드)들이 로봇의 상태도 표현하고 장애물의 위치도 표현하는 방식이다. 일반적인 grid 기반의 A*에서는 로봇이 바라보는 방향에 대한 고려 없이 xy좌표만을 로봇의 상태로 고려한다.
그래서 이산화된 격자를 대표하는 질점과 질점을 연결해 가면서 장애물을 회피하는 가장 짧은 최종 경로를 계획하게 된다.
이 방법의 장점은 cost function이나 heuristic function을 내가 원하는 대로 설정함으로써 내가 뭘 더 중요시하는지 짧은 길인지 안전한 길인지 빠른 길인지 정의할 수 있으며 이를 통해 내 path planner의 퍼포먼스를 결정할 수 있다는 점이다. 이러한 단순함과 퍼포먼스 때문에 홀로노믹 로봇의 패스 플레이닝에 많이 사용되는 알고리즘이다.
A* 알고리즘의 작동 과정
알고리즘의 작동을 순서대로 나타내자면 아래와 같다.
Step 1: Mark all nodes unvisited. Create an unvisited set.
Step 2: Calculate distances of all its unvisited neighbors through the current node
Step 3: Compare the newly calculated distance to the current assigned value and assign the smaller one.
Step 4: Compute cost of all the unvisited neighbors of the current node.
Step 5: Mark the current node as visited
Step 6: Set the unvisited node with the smallest cost as the new "current node”
Step 7: Go back to step 2.
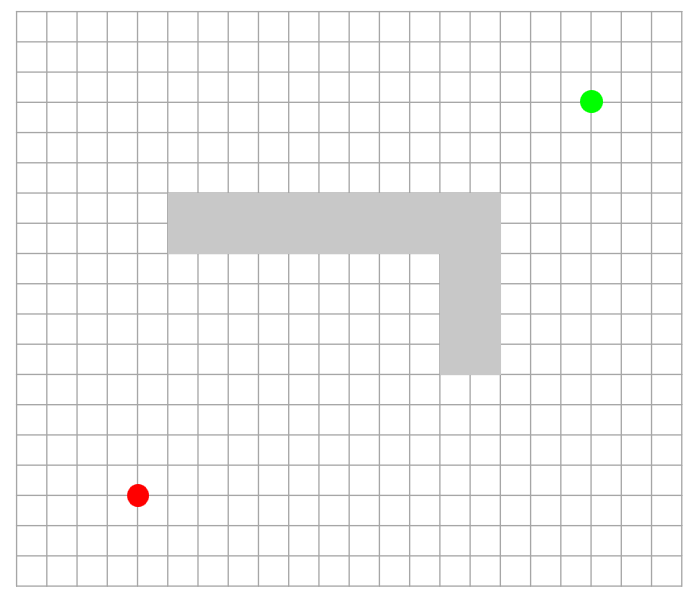
그림 3. 알고리즘 Step 1. 초기 상태에서는 아무 곳도 방문하지 않았다고 본다.
먼저 그리드로 나눠져 있는 공간이 존재 하고 빨간색 시작점 녹색 종료점, 그리고 회색의 장애물이 보인다.
시작할 때, 그리드 위의 모든 노드는 방문 안한 노드 즉, unvisited로 설정한다.
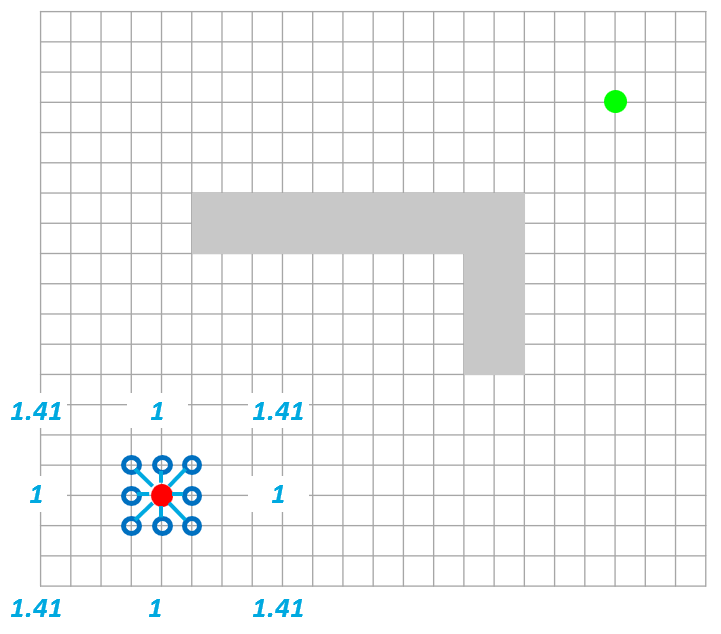
그림 4. 알고리즘 Step 2. 이웃한 노드로 갈 때 소요되는 cost (여기서는 거리)를 계산한다.
그리고 시작점을 먼저 current node 즉, 현재 검색을 수행하는 점으로 지정해서 Current node 주변의 8개 점까지 거리를 계산한다. 여기서는 대각선 움직임도 허용해서 대각선 움직임의 거리는 좀 다르게 설정하였다. 그리고 이 거리값을 시작점부터 current node까지 거리와 더해 시작점부터 해당점까지 도달하는 거리를 계산한다.
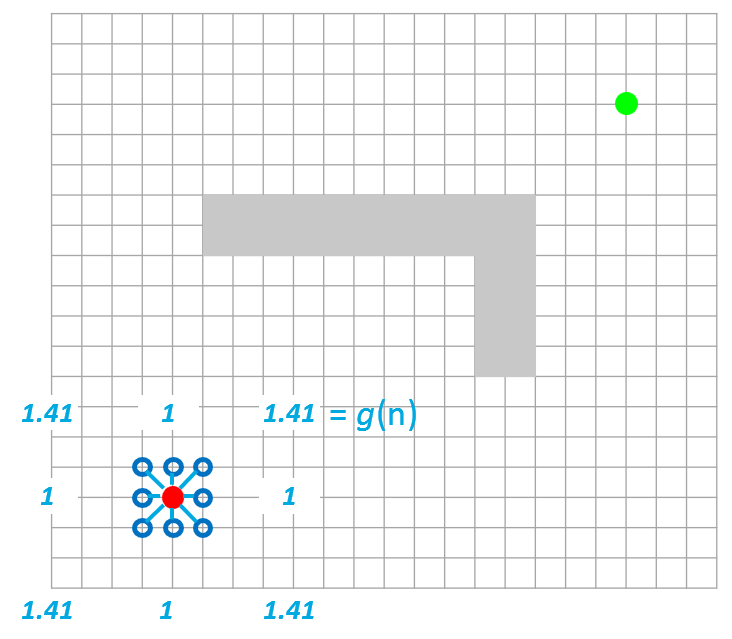
그림 5. 알고리즘 Step 3. 이웃한 노드까지의 거리를 기반으로 한 cost를 비교하여 가장 작은 값을 갖는 노드를 선택한다.
그리고 주변 점들 중 시작점으로 부터의 거리를 가진 점이 있다면 둘 중 작은 값으로 거리값을 업데이트 한다. 이 거리 값은 경로의 시작점으로부터 현재 고려하고 있는 주변점까지의 경로에 종속적인 거리이다. 다시 말해, cost는 경로에 종속적이기 때문에 다른 경로를 통해 이 점에 도착하면 그 거리값이 다를 수 있다는 것이다. 하지만, 지금은 첫 시작이기 때문에 current node로 부터의 거리만 있다. 그래서 구해진 값을 바로 업데이트하면 된다.
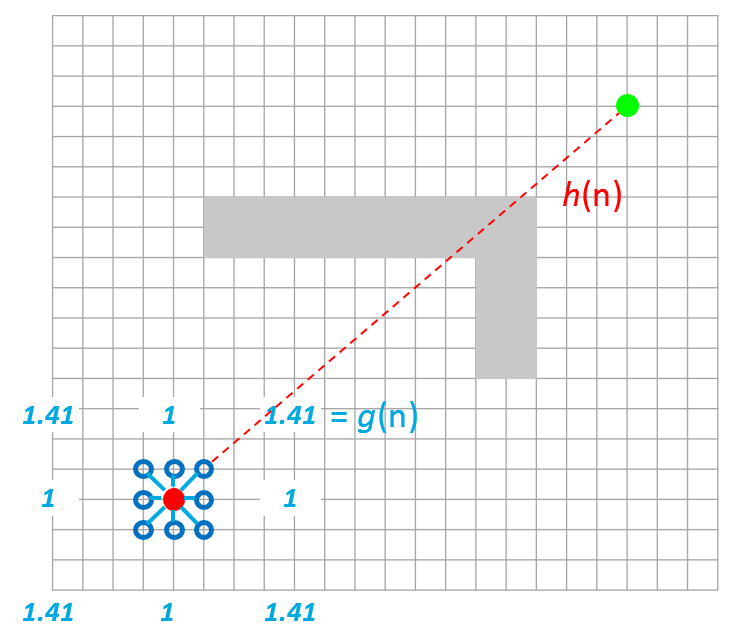
그림 6. 알고리즘 Step 4. 이웃한 노드까지의 거리를 기반으로 한 cost를 비교하여 가장 작은 값을 갖는 노드를 선택한다.
이제 주변 점들에 대한 total cost를 구한다. Total cost는 시작점에서 cost를 계산하는 점까지의 미리 구해놓은 거리 $g(n)$과 이 점에서 목적지까지의 장애물을 고려하지 않은 최단 거리인 heuristic $h(n)$을 더해서 구해진다. 결국 이 total cost가 낮은 방향으로 추가 공간 검색이 이루어진다.
Heuristic이 작은 걸 선택을 하려고 하면 아무래도 목표점에 가까운 점을 선택하려고 할 것이므로 $g(n)$과 $h(n)$을 더한다는 것은 결국 추가 검색의 방향성을 제공한다는 의미가 된다. 그리고 나면은 이제 current node에 대해서는 알아볼만큼 다 알아봤으니 더 이상 이 점에 대해서는 추가검색을 하지 않겠다는 의미로 visited로 전환한다. 그리고 나면 주변의 점들 중에서 unvisited 이자 가장 작은 total cost값을 가진 점을 다음 프로세싱을 위한 current node로 전환하고 다시 2번 step부터 반복수행한다. 그럼 장애물을 만나도 장애물을 회피하여 공간을 검색하고 최종적으로 목적지에 도달하는 경로를 찾게 된다.
Navigation toolbox에서는 plannerAStarGrid 함수에 grid map을 입력하여 planner를 만들고, 시작점과 끝점을 입력해서 경로를 탐색하는 기능을 제공하고 있다. 아래는 그림 2에서 활용한 예시 매트랩 코드이다.
% Define a grid map
map = mapClutter;
% Create A* planner
planner = plannerAStarGrid(map);
% Plan a path from start point
% to goal point
start = [2 3];
goal = [248 248];
plan(planner, start, goal);
% Visualize the planned path
show(planner)
그래프 기반 A*
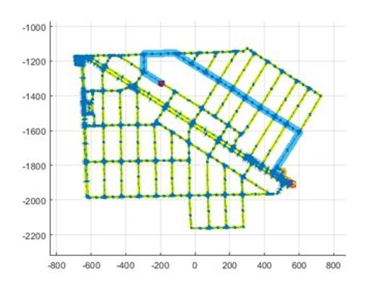
그림 8. 그래프 기반 A* 플래너의 활용 예시
이 시리즈 비디오의 첫시간에서도 언급했지만, Route planning은 planning 복잡도를 낮추기 위해 넓은 범위부터 좁은 범위로 단계를 나누어 path planning을 할 때 가장 넓은 범위에서 경로를 계획하는 과정이라고 언급한 바 있다.
만약, 집, 사무실, 공장과 같이 로봇의 활동범위가 좁은 application의 경우에는 전체 활동 영역을 grid로 만들어도 그 크기가 크지 않을 수 있어 맵을 저장하는데 필요한 메모리도 비교적 작고, 검색 영역도 좁아 금방 경로를 만들수 있지만, 자율주행차와 같이 넓은 영역에서 경로를 만들어야 하는 경우 맵을 저장하기 위한 메모리도 너무 커지고, 검색영역도 너무 넓어 route planning에 너무 많은 시간이 소비될 수 있다.
이를 위해 자율주행 같은 시스템에서는 같은 A* 알고리즘을 사용하지만 맵은 grid가 아닌 graph를 이용하게 된다. Graph는 점 즉 node와 점 사이를 연결하는 링크 즉 edge로 네트워크를 표현하는 표현 방식이다. 실제로 여러분이 차에서 사용하는 navigation도 이런 graph 방식으로 표현되어 있다. 이 방법을 이용하면 맵을 표현하는데 사용하는 메모리도 줄일 수 있고, 점과 점사이의 연결에 대해서만 경로를 검색하면 되니까 route planning 속도도 빠르다.
이를 위해서 navigation toolbox 에서는 두개의 함수를 제공하고 있다. 첫번째는 graph 형태의 map object를 표현하기 위한 navGraph 함수이고, 다른 하나는 이렇게 만들어진 graph 형태의 map 위에서 A* 알고리즘을 수행하는 plannerAStar 함수이다. 그러면 navGraph와 plannerAStar의 두 가지 함수가 어떤 식으로 사용되는지 보도록 하자.
Design Case 1
일단 첫 번째는 굉장히 단순한 route planning 예제를 다루어보자.
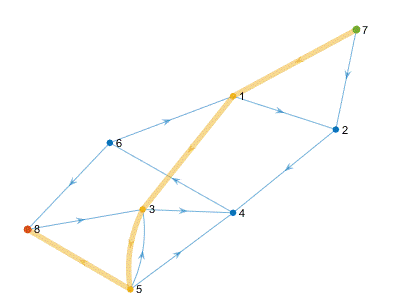
그림 9. 아주 단순한 route planning 예제
여기서는 그림과 같이 노드 8개가 있다. 먼저 이 점들을 먼저 정의하자. 그래서 아래의 매트랩 코드에서 볼 수 있는 것 처럼 노드는 60,70 … 80,60 이런 식으로 XY의 쌍으로서 하나의 노드를 표현해서 8개의 노드를 표현했다.
% Nodes of the graph conntaining (x,y) locations
nodes = [60,70;85,60;38,36;60,35;35,12;30,56;90,90;10,30];
그 다음은 엣지를 표현한다. 우리가 지금 좌표를 넣은 순서대로 노드 1번 점 2번 3번 이렇게 지정을 하게 되는데 엣지의 시작점 끝점 이런 쌍으로서 하나의 엣지를 표현을 해주는 것이다.
% Edges containing the [start end]
edges = [1,2;1,3;2,4;3,4;3,5;5,3;5,4;4,6;6,1;6,8;7,1;8,3;7,2;5,8];
그러고 나면 navgraph 오브젝트에 이 노드 정보와 엣지 정보를 넣어서 오브젝트를 구성을 하게된다.
% Create navGraph Object
navGraphObj = navGraph(nodes, edges);
그리고 이 맵 정보를 plannerAStar 함수에 또 집어넣게 되면 이제부터 이 플래너 오브젝트는 navgraph 맵 위에서 route planning을 수행한다.
% Create graph-based A* planner
planner = plannerAStar(navGraphObj);
이제 본격적인 패스 플레이닝을 한번 해보자. 일단 시작점 끝점을 정의한다. 지금은 좌표 값으로 시점과 종점을 정의했는데, 시작점을 보면 미리 정의한 노드들의 위치하고 스타트 포인트가 똑같은 값이 존재하지 않는다는 것을 알 수 있다. 결국 스타트 포인트라고 내가 지정해준 좌표에 가장 가까운 노드에서부터 종료점 포인트에 가장 가까운 노드까지 planning을 해주는 그런 결과를 얻게 되었다.
% Start and goal node states
start = [90.5, 90.5];
goal = [10.5, 30.5];
% Find the shortest path using graph-based A* algorithm
[pathOutput, solnInfo] = plan(planner, start, goal);
이 예제의 포인트는 결국 (1) 노드, 엣지 정보를 벡터 데이터로 입력해 graph를 만들 수 있다는 점과 (2)그 그래프 위에서 planning을 할수 있다는 점 두가지로 생각할 수 있겠다.
% Nodes of the graph conntaining (x,y) locations
nodes = [60,70;85,60;38,36;60,35;35,12;30,56;90,90;10,30];
% Edges containing the [start end]
edges = [1,2;1,3;2,4;3,4;3,5;5,3;5,4;4,6;6,1;6,8;7,1;8,3;7,2;5,8];
% Create navGraph Object
navGraphObj = navGraph(nodes, edges);
% Create graph-based A* planner
planner = plannerAStar(navGraphObj);
% Start and goal node states
start = [90.5, 90.5];
goal = [10.5, 30.5];
% Find the shortest path using graph-based A* algorithm
[pathOutput, solnInfo] = plan(planner, start, goal);
% Visualize results
h = show(navGraphObj);
PathStateIDs = solnInfo.PathStateIDs;
highlight(h, PathStateIDs, EdgeColor='r', NodeColor='r');
highlight(h, PathStateIDs(1), NodeColor='#77AC30', MarkerSize=10);
highlight(h, PathStateIDs(end), NodeColor='#D95319', MarkerSize=10);
Design Case 2
두 번째는 조금 더 복잡하게 한번 해보자. 아래 그림 10과 같은 맵이 있다고 생각해보자. 관련 예제의 링크: 링크
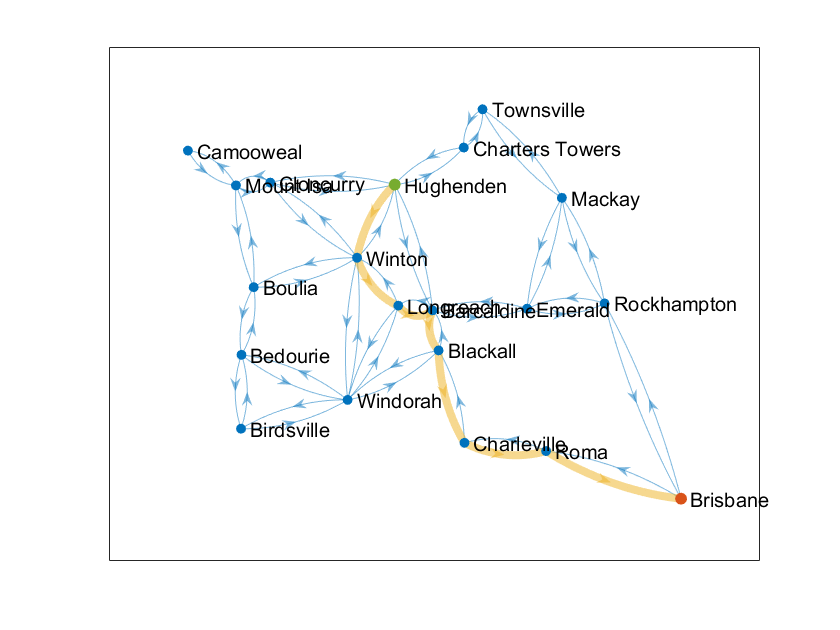
그림 10. 조금 더 복잡한 route planning 예제
그림 10에서 볼 수 있는 것 처럼 이번 예시에서는 노드들이 이름을 가지고 있다. 그리고 이 노드들의 이름을 사용해서 a라는 노드에서 b라는 노드로 planning 하도록 하자.
아래의 매트랩 코드에서 볼 수 있는 것 처럼 load 함수를 이용해서 그래프 정보를 가져온 뒤 관련 정보를 state, names, links, weight 이런 변수에다가 차례로 저장한다. 그래서 state와 name은 하나의 행이 같은 노드의 정보를 표현하는 것이다. 그리고 링크 정보도 시작점 끝점 그리고 거기에 대한 웨이트를 가지고 있다.
% Load the Queensland road network.
load("queenslandRoutes","places","routes")
% Specify states, links, and weights for a |navGraph| object.
states = places.utm; % UTM coordinates of cities
names = places.name; % Names of cities
links = [routes.start routes.end]; % Adjacent cities
weights = routes.time; % Travel time between adjacent cities
그래서 아래 코드와 같이 navGraph를 만들 때 이번에는 노드 엣지만 넣는 게 아니라 웨이트와 네임도 같이 넣을 수 있는 옵션을 이용해서 같이 넣은 것을 알 수 있다.
graphObj = navGraph(states,links,Weight=weights, Name=names);
그리고 planner도 동일한 방법으로 만든다.
여기서 Design Case 1과 다른 점은 heuristic 함수를 임의로 지정한다는 것이다.
planner.HeuristicCostFcn = @(state1,state2) sum(abs(state1-state2),2)/100;
만약 이렇게 하지 않았다면 현재 검색 위치에서 종료점까지 거리를 계산하는 기본적인 A* 형식으로 heuristic을 계산할텐데 이런 식으로 함수를 만들어 놓으면 원하는 형태의 heuristic을 사용해서 path planning의 결과를 내가 원하는대로 조정할 수 있다.
그러면 스타트 포인트 및 골 포인트를 정하는데 이번에는 좌표가 아니라 노드의 이름을 사용했다. 그리고 planning해서 그 결과를 찍어보면 그림 10과 같이 나타난다.
% Define the start and goal cities.
start = "Hughenden";
goal = "Brisbane";
% Find the shortest path using the graph-based A* algorithm.
[pathOutput,solutionInfo] = plan(planner,start,goal);
이 예제의 포인트는 (1) heuristic function을 원하는 형태로 바꿔서 사용할 수 있다는 것과 (2) 노드의 이름이 있다면 노드의 이름을 사용해서 planning 할 수 있다는 것이다. (관련 문서의 링크)
아래는 전체 코드이다.
%% Plan Shortest Path Between Two States in Graph Using A-Star Path Planner
% Load the Queensland road network.
load("queenslandRoutes","places","routes")
% Specify states, links, and weights for a |navGraph| object.
states = places.utm; % UTM coordinates of cities
names = places.name; % Names of cities
links = [routes.start routes.end]; % Adjacent cities
weights = routes.time; % Travel time between adjacent cities
% Create a navGraph object.
graphObj = navGraph(states,links,Weight=weights, Name=names);
% Create a graph-based A* path planner.
planner = plannerAStar(graphObj);
% Create a deep copy of the |plannerAStar| object.
planner2 = copy(planner)
% Specify a heuristic function returns an estimated time to reach the goal.
planner.HeuristicCostFcn = @(state1,state2) sum(abs(state1-state2),2)/100;
% Define the start and goal cities.
start = "Hughenden";
goal = "Brisbane";
% Find the shortest path using the graph-based A* algorithm.
[pathOutput,solutionInfo] = plan(planner,start,goal);
% Visualize the results.
h = show(graphObj);
set(h,XData=graphObj.States.StateVector(:,1), ...
YData=graphObj.States.StateVector(:,2))
pathStateIDs = solutionInfo.PathStateIDs;
highlight(h,pathStateIDs,EdgeColor="#EDB120",LineWidth=4)
highlight(h,pathStateIDs(1),NodeColor="#77AC30",MarkerSize=5)
highlight(h,pathStateIDs(end),NodeColor="#D95319",MarkerSize=5)
Design Case 3
그러면 이제 좀 더 실질적인 예제를 보자.
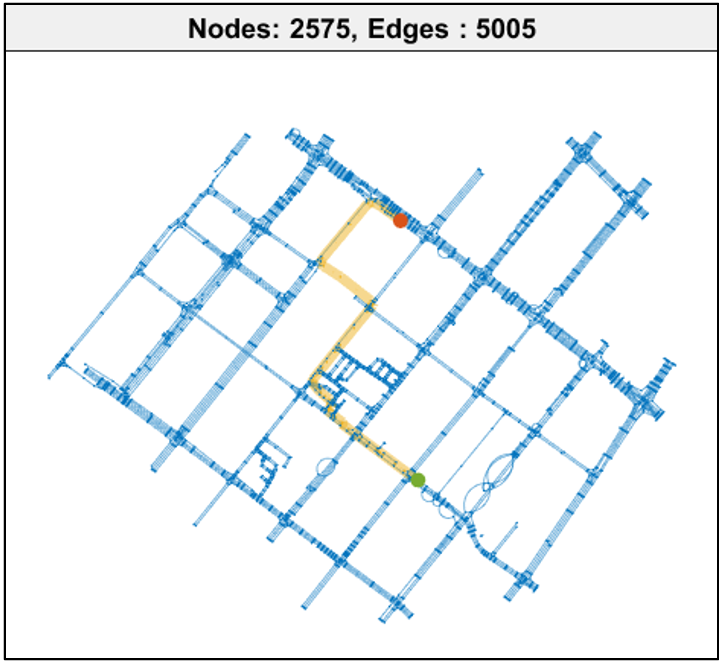
그림 11. LA 어딘가의 구역에서 얻어온 HD Map
그림 11은 차선 수준의 연결성 정보를 갖고 있는 실제 HD 맵이다.
처음에는 이 HD Map 정보를 불러온다. 그리고 여기서 그래프를 만들기 위한 정보를 추출해서 그래프를 만든다. 정보를 추출하는 함수 HDMapToStatesLinks는 HD Map의 형태에 따라 다를 수 있는 것이기 때문에 크게 중요한 것은 아니다.
% Load HD map data
load("test23LosAngeles", 'LanesStruct', 'xMid', 'yMid')
[statesTable, linksTable] = HDMapToStatesLinks(LanesStruct, xMid, yMid);
% Create graph
nGraph = navGraph(statesTable, linksTable);

그림 12. LA 어딘가의 구역에서 얻어온 HD Map
그림 12에서 볼 수 있는 것 처럼 node 와 edge 데이터를 stateTable과 linkTable 라는 이름의 테이블 형식을 사용한 것을 알 수 있다. 이전의 예제에서 node와 edge 정보는 vector 데이터 형태를 사용했지만, 여기서는 table형 이 사용된 것이다. Table 데이터 타입은 MATLAB에서 제공하는 또 다른 형태의 데이터 타입인데, 엑셀 스프레드시트처럼 열에 이름을 붙이고 접근해서 관리할 수 있다.
그래서 state 테이블에는 노드의 위치 정보만 있는 게 아니라 거기에 해당되는 추가적인 특성값들을 같이 넣어두었다. 마찬가지로 링크도 그런 식의 정보들을 갖다 같이 넣어둔 것을 알 수 있다. 결국 이 정보들은 사용자가 원하는 heuristic이나 weight 함수를 만드는데 사용될 수 있다.
% Set cost function
W = [20,10,0.05]; % cost function weights
nGraph.LinkWeightFcn = @(id1, id2, nGraph) HDMapCostFcn(id1, id2, nGraph, W);
% Create plannerAStar object
planner = plannerAStar(nGraph);
planner.HeuristicCostFcn = @(ind1, ind2) ...
W(3)*nav.algs.distanceManhattan(ind1, ind2);
% Plan path
start = 525;
goal = 434;
[pathOutput, solnInfo] = plan(planner, start, goal);
% Visualize results
h = show(nGObj);
이 예제에서는 cost function을 만드는데 이 값들이 사용된 것을 알 수 있다. 여기서는 cost function이 graph object의 weight function으로 나타나는데 원래 default는 경로에 종속적인 거리 정보였다면 이제는 사용자가 정한 함수를 이용해서 weight 값을 설정해서 cost로 사용할 수 있다.
그리고, a*함수에서는 heuristic 함수도 앞의 예제와 같이 수정했다. 그럼 결과가 그림 11과 같이 나온다. 노드가 2575개이고, edge가 5000개가 넘는 지역에서 손쉽게 route planning을 수행한 것을 알 수 있다.
이 예제에서의 포인트는 “엑셀과 같은 스프레이드 시트 형태로 정리된 데이터를 사용해가지고 이제 그래프를 구성하실 수도 있다.”는 점과 “cost 펑션도 사용자 정의하여 원하는 형태로 route planning 결과가 나오도록 여러 옵션을 고려할 수 있다.” 라는 점이다.
여기까지 맵에서 정보를 추출해와서 planning을 위한 graph map을 만들고 이 위에서 route planning을 하는 방법에 대해 알아보았다. 그러면 다음 시간에는 또 다른 global path planning 방식에 대해 얘기를 해보도록 하자.
Technical Resources
정리하면 이 비디오에서는 Navigation Toolbox에서 제공하는 global path planning 알고리즘의 종류와 그중 route planning에 주로 사용되는 graph 위에서 A* 알고리즘을 사용하는 방법에 대해 알아보았다. Path Planning 분야 외의 로봇 개발을 위한 다른 내용이 궁금하다면 아래의 매스웍스 코리아에서 제공하는 모바일 로봇틱스 그리고 자율주행 웹 포털을 통해 정보를 얻어갈 수 있으니 참고하기 바란다.
MATLAB Mobile Robotics Web Portal

그림 13. MATLAB을 이용한 육상 이동 로봇 개발 Web Portal (링크)
MATLAB ADAS Web Portal

그림 14. MATLAB을 이용한 자율주행/ADAS 개발 Web Portal (링크)
MATLAB Onramp Series
매트랩 기초 사용법을 학습하고 싶은 경우 MathWorks 홈페이지 내의 Onramp 라는 무료 트레이닝 코스를 활용할 수 있다. Onramp는 웹상으로 진행하는 온라인 무료 교육으로, 컴퓨터에 매트랩을 설치 할 필요 없이 온라인으로 매트랩 관련된 여러 기초 내용을 학습할 수 있다.
그림 15. MATLAB을 무료로 배울 수 있는 Onramp 시리즈 (링크)