본 포스팅은 아래의 MathWorks 김종헌 프로님의 Path Planning 시리즈 중 아래의 비디오를 정리한 것입니다.
이 비디오에서는 모바일 패스플래닝 시리즈 비디오의 두번째 파트로 MATLAB에서 제공하는 path planner를 사용함에 있어 기본이 되는 몇가지 요소들 대해서 설명한다. 그 첫 번째 시간으로 Motion Primitive에 대해서 설명한다.
Motion Primitives
Motion Primitive 란 로봇이 취할 수 있는 모션이다.
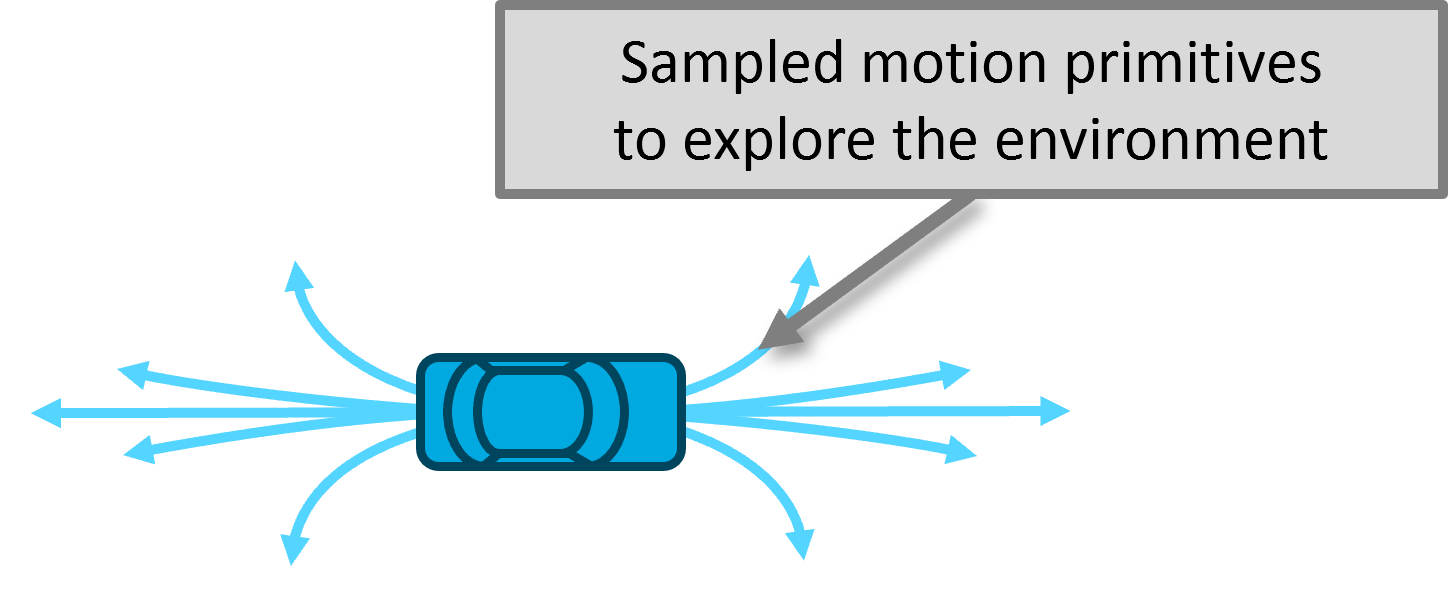
그림 1. 자동차가 취할 수 있는 몇 가지 Motion Primitives의 시각적 예시
위와 비슷한 Motion Primitive를 미리 구성해두고, Motion Primitive를 조합해서 좀 더 복잡한 형태의 전체 패스를 생성하거나 path planning 알고리즘이 공간을 탐색할 때 공간을 샘플링하는 용도로 사용하게 된다.
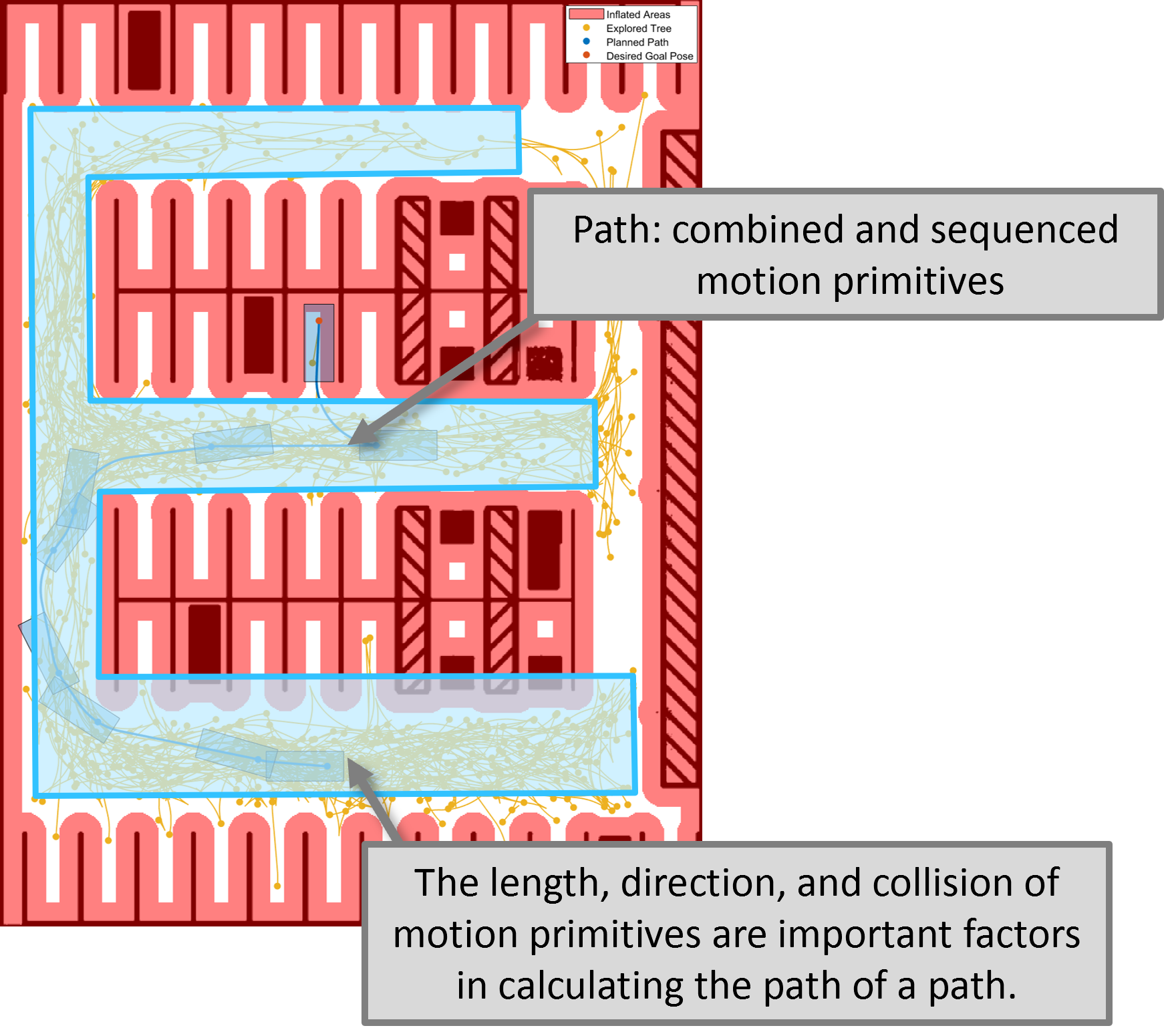
그림 2. 일련의 Motion Primitive를 조합하여 얻게되는 샘플 경로 예시
Motion Primitive의 조합으로 공간을 샘플링하면 전체 패스를 생성할 때, 공간을 검색할 때, 연산량을 줄여 연산에 소모되는 시간을 최소화할 수 있다. 공간을 샘플링할 때 내가 사용하는 로봇이 취할 수 없는 접근 불가한 모션을 샘플링하는 게 아니라 실제로 로봇이 구현 가능한 모션을 샘플링 해야 되기 때문에 이러한 motion primitive를 미리 계산하여 공간을 sampling하게 된다. 그리고 어떤 경로가 결정이 됐을 때 이 경로가 최적 경로인지 아닌지 확인하기 위해 경로 추종에 대한 비용을 계산하여 다른 경로와 비교를 할 때도 Motion Primitive가 사용된다.
Motion Primitive를 이런 업무에 활용하기 위해서는 어떤 특징을 가져야 할까? 우리는 Motion Primitive를 조합해서 더 복잡한 형태의 패스를 만들어낼 것이기 때문에 (1) motion primitive의 형상이나 표현 방법이 복잡하면 안 된다. Motion Primitive 자체는 단순해야 그 다음 이것들이 조합했을 때의 패스도 최대한 단순하게 표현할 수 있기 때문에 심플하게 표현되어야 한다. 또, Path planning을 하는데 있어 반복적으로 많이 사용되기 때문에 (2) 재사용성을 가지도록 설계되어야 한다. 하지만, motion primitive를 조합하는 형태로 path가 계획되며 계획된 path의 품질 그 중에서도 smoothness에 영향을 주기 때문에 (3) 최대한 robot 모션의 품질을 높이기 위해 최대한 smooth한 형상을 가지고 있어야만 한다.
Kinematic Constraints
결국 로봇이 가질 수 있는 모션을 “간단하게” 표현한다는 것은 내 로봇이 가지고 있는 kinematic constraints를 표현한다는 말과도 같다. Kinematic constraints는 로봇이 어떤 방향이든지 가고 싶은 방향으로 움직이는 데 있어서 모션에 가해지는 제약을 말한다. 여기서, 내가 원하는 모든 방향으로 다 갈 수 있는 형태를 omni-directional 혹은 holonomic system이라고 하고 그렇지 않은 시스템을 non-holonomic system이라고 한다.
이 non-holonomic system을 정확하게 정의하자면, 로봇이 가지고 있는 자유도보다 컨트롤 input에 대한 자유도가 더 적은 시스템을 non-holonomic system이라 말한다.
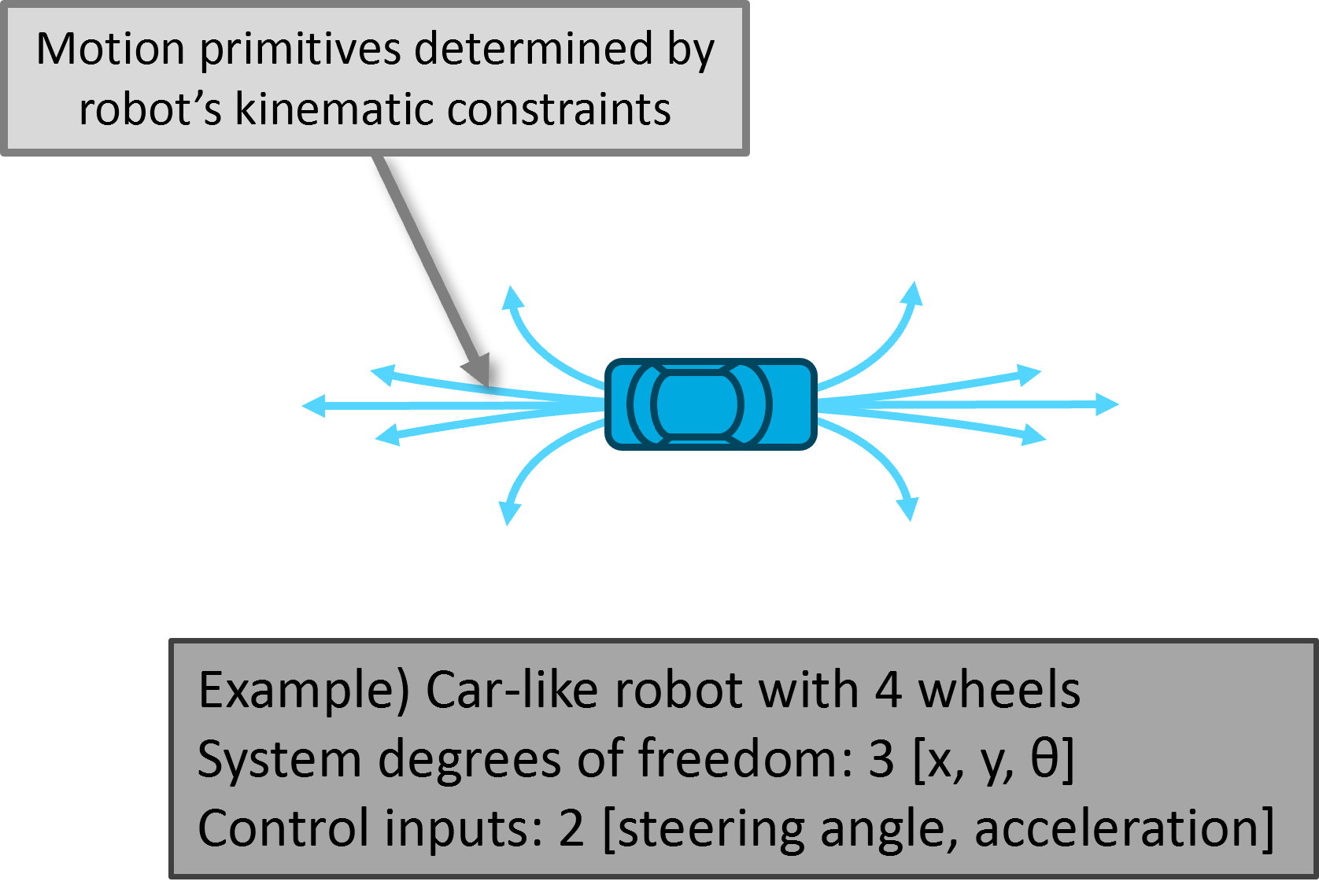
그림 3. 자동차 움직임의 자유도와 kinematic constraints
예를 들어, 자동차의 경우 그림 3에서 볼 수 있는 것처럼 2차원 평면에서 움직이는 자동차가 가질 수 있는 자유도는 $[x, y, \theta]$ 세 가지이다. 이 때, 우리가 이 차를 움직일 때 줄수 있는 제어 인풋은 전후 방향으로 움직이게 하는 acceleration과 스티어링 앵글 둘 뿐이다. 즉, 로봇이 가지고 있는 자유도는 3인데, 컨트롤 인풋에 의한 자유도는 2에 불과하다. 이런 차의 움직임 메커니즘을 “Ackermann steering mechanism“이라고 하는데, 이러한 메커니즘을 가진 로봇은 측면방향으로 바로 움직일 수 없고 같은 자리에서 바로 회전할 수도 없다.
정확하게 동일하지는 않지만, 대부분의 모바일 로봇 플랫폼들은 유사한 형태의 움직임에 대한 제한 조건을 가진 non-holonomic system인 경우가 많다. 많이 사용되는 바퀴간의 회전 속도와 방향의 차이로 steering을 수행하는 differential robot도 non-holonomic system의 일종이다. 결국은 이런 non-holonomic 시스템들에 대한 path planning을 수행하려면 움직임에 제한이 있으니 이러한 kinematic constraint를 고려해서 Path planning을 수행해야하고, path를 구성하는 motion primitive 레벨에서 이미 kinematic constraint를 고려해야 한다.
Motion Primitives for a Non-Holonomic System
그럼, Non-holonomic system을 위한 motion primitive는 어떤 것들이 있을까?
Dubins Path
먼저 Dubins 모델은 시작 pose에서 완료 pose까지 우회전, 좌회전, 직진 3개의 움직임을 3번 조합하여 최적 경로를 만들어 내는 방법이다. 참고로 여기서 우회전과 자회전은 모두 Maximum Steering으로 회전하는 경우를 상정한다. 두 pose는 수학적으로 RSR, RSL, LSR, LSL, RLR, LRL의 총 6가지 모델 중 하나로 반드시 연결될 수 있다.
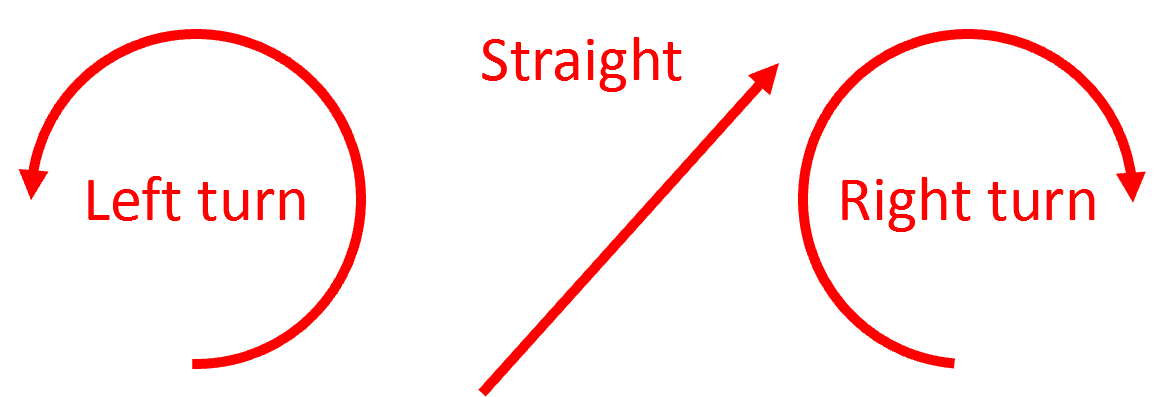
그림 4. Dubins 모델의 Motion Primitives (L, S, R)
어떻게 연결될 수 있는지 예를 들어 보자. 아래 그림 5에서는 시작 pose(파란색 화살표)와 완료 pose(초록색 화살표) 사례 두가지가 있다. 그림 5의 왼쪽부터, 시작 및 완료 pose 간의 관계는 좌선회, 직진, 다시 좌선회해서 연결되므로 이것을 LSL type의 움직임이라고 한다. 그림 5의 오른쪽에서는 우선회, 직진, 좌선회해서 연결되므로 이것을 RSL type의 움직임이라고 한다.
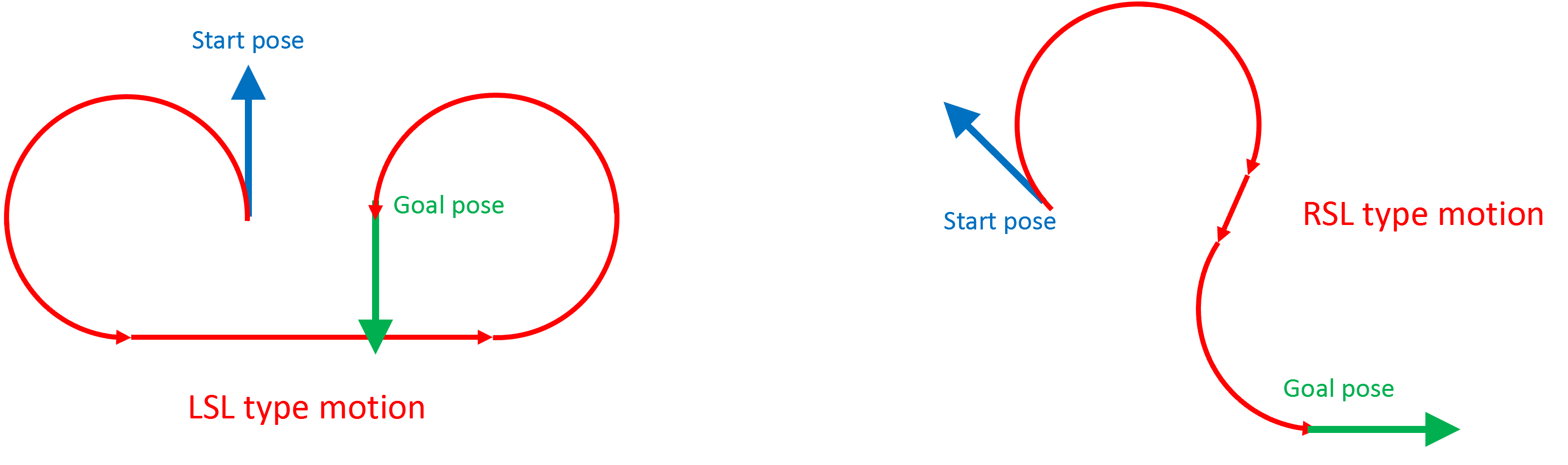
그림 5. Dubins 모델의 Motion Primitives 연결 예시 (LSL, RSL)
이런 움직임을 갖는 제일 흔한 예는 비행기이다. 후진이 불가능한 비행기가 방향을 바꿔서 반대로 넘어가려고 그러면 크게 우선해서 삥 두르면 저런 식으로 방향을 돌릴 수도 있다. 하지만, 이걸로는 부족하다. 비행기면 모르겠지만 창고 물류 로봇이나 주차하는 차량처럼 한정된 공간에서 공간과 에너지를 효율적으로 사용하려면 후진이 가능해야 한다.
Reeds-Shepp Path
그래서 Dubin path 모델의 아이디어를 확장해서 후진까지 고려할 수 있도록 개발한 것이 바로 Reeds-Shepp 모델이다. 이 방법도 직진(Straight), 좌선회(Left turn), 우선회(Right turn)로 표현되는 데 여기에 움직임 없음 N도 추가된다. Dubins 모델에서와 마찬가지로 우회전과 자회전은 모두 Maximum Steering으로 회전하는 경우를 상정한다. Reeds-Shepp는 이 움직임들을 5회 조합해서 연결을 하는데 3회만에 원하는 목적지에 연결되는 경우에는 굳이 네번째, 다섯번째 움직임이 필요 없어서 N으로 표현된다. 여기에 전진, 후진을 각각 +와 -의 부호로 각각 표현해서 총 48개의 움직임 조합으로 두 개의 pose를 연결하는 방법을 구현하였고, 나중에 그 중 불필요한 2개(L- R+ L-, R- L+ R-)를 제거해 최종적으로 46가지 움직임이 아래 표와 같이 조합된다.

그림 6. Reeds-Shepp Motion Primitives의 조합
출처: Steven M. LaValle. Planning Algorithms. Cambridge University Press, 2006.
그래서 하나의 예를 또 들어보자면, 그림 7과 같은 상황에서 주차를 하기 위해 두 개의 pose를 연결하려면 이렇게 R+ L- S- R- N 순서의 움직임으로 표현할 수 있다.
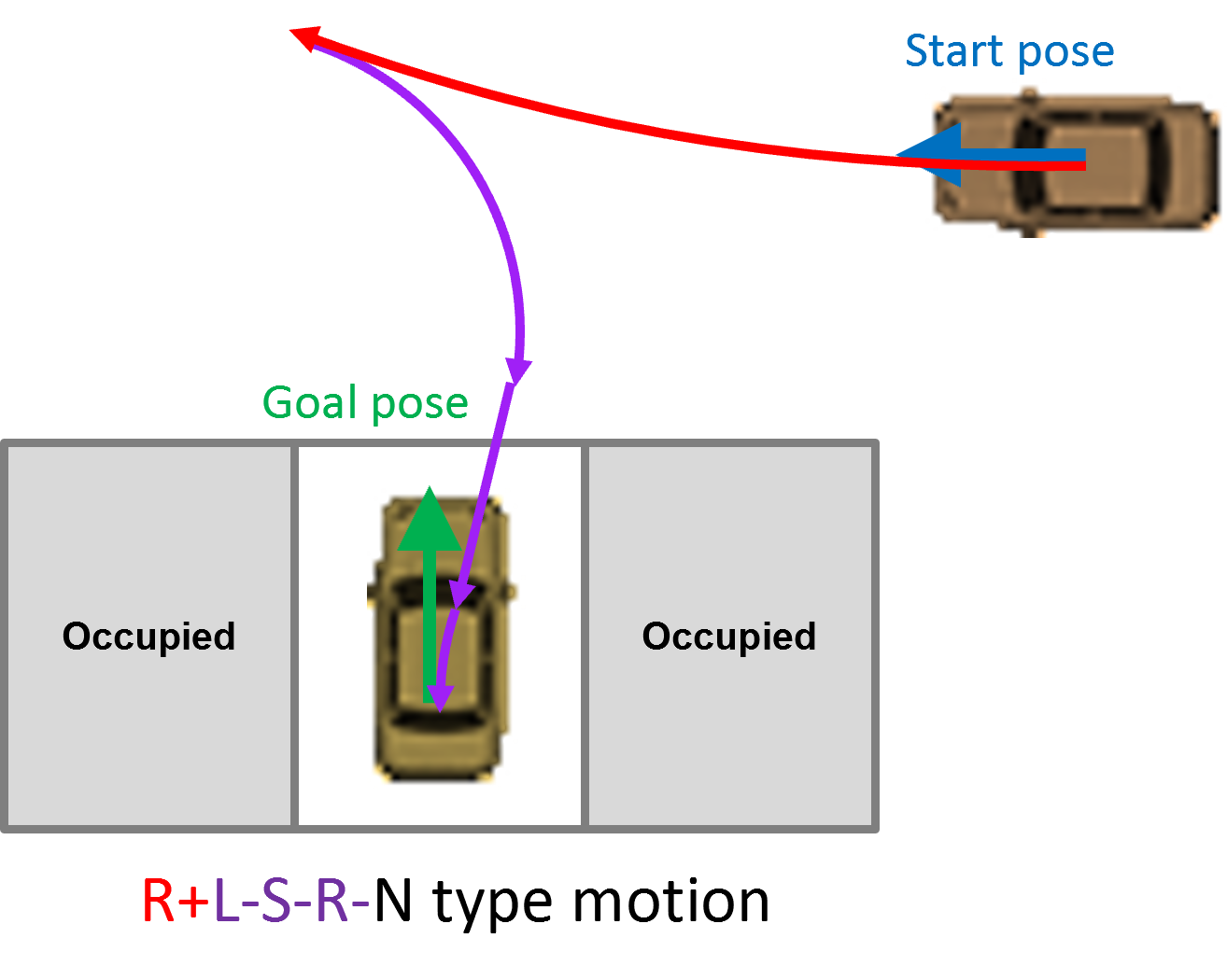
그림 7. Reeds-Shepp Motion Primitives의 조합 예시 (R+ L- S- R- N)
Ground Vehicle Motion Primitives in Navigation Toolbox
MATLAB의 Navigation Toolbox에서는 navPath(직선 조각), Durbin Path와 Reeds-Shepp Path 세 가지 motion primitive를 제공한다. 이 함수들은 가능한 여러 motion primitive에서 가장 효율적인 연결 primitive만 제공하는게 아니라 이렇게 연결된 motion primitive를 시각화하는 함수도 같이 제공한다. 그리고 함수를 직접 사용하는게 아니더라도 나중에 패스 플래닝 함수들에서 옵션을 선택함으로써, 알고리즘 내부에서 공간을 sampling하는데 사용하고 생성된 path들이 motion primitive의 조합으로 발생하게 된다.
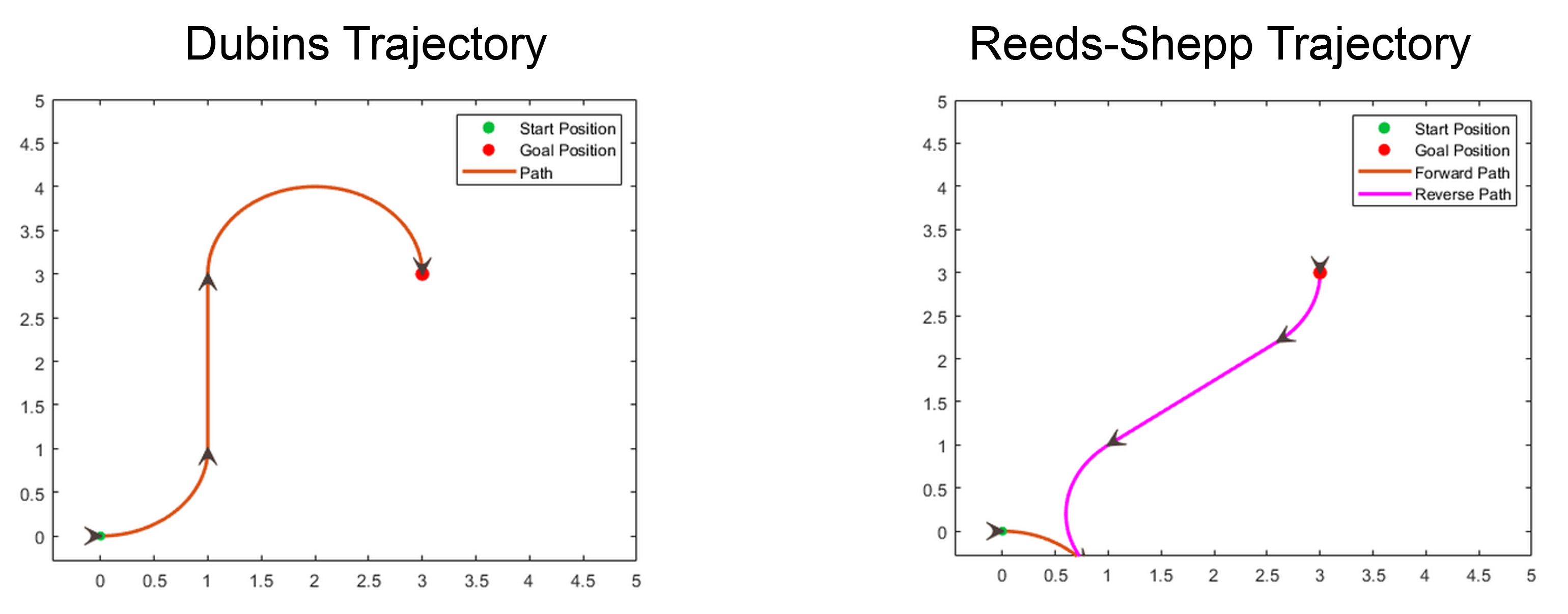
그림 8. MATLAB에서 동일한 두 pose를 Dubins 방식과 Reeds-Shepp 방식으로 연결시킨 결과
navPath object
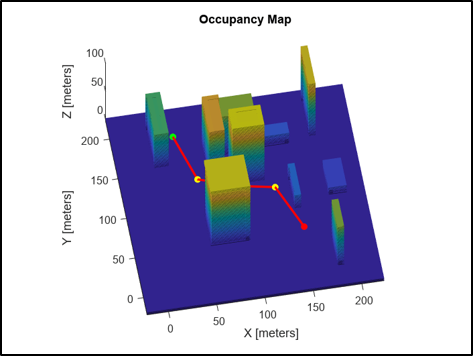
그림 9. navPath 오브젝트로 구성한 Path 결과물 (소스 코드 링크)
그럼 가장 첫 번째 navPath 오브젝트에 대해서 알아보자. navPath 오브젝트는 그냥 바로 직선적으로 연결하는 패스 오브젝트이다. Append, interpolate, path length 같은 메소드들을 제공을 하고 있다.
| methods | |
|---|---|
| Add states to end of path | |
| Interpolate points along path | |
| Length of path |
% Create an SE(3) with bounds for state variables.
ss = stateSpaceSE3([0 220;0 220;0 100;… % x-,y-,z- min/max
inf inf;inf inf;inf inf;inf inf]); % qx-,qy-,qz- min/max
% Create a navPath object in an SE(3) state space.
path = navPath(ss);
waypoints = load("waypoints.mat"); % Load waypoints
append(path, waypoints);
interpolate(path,250); % Interpolate that path evenly.
% Visualize the interpolated path and the original waypoints.
omap = load("dMapCityBlock.mat"); % Load a 3D occ map
show(omap); axis equal; view([-10 55]); hold on; plot3(path.States(:,1),path.States(:,2),path.States(:,3), "r-”);
% Calculate length of path.
len = pathLength(path);
코드를 보면 어떤 공간 안에서 state space를 먼저 정의하게 된다. 여기서는 SE3 스테이트 스페이스로 정의하고 x,y,z 그리고 또 방위에 관련된 스테이트들에 대해서 min / max 바운더리를 정해준다. 그리고 SE3 state space에서 motion primitive의 object를 생성한다.
그런 뒤 방금 언급한 append method를 사용해서 waypoint를 추가하고 interpolate 메소드를 이용해 균일한 간격으로 250개 구간으로 쪼개면 이 object는 250개의 state 값을 가진 path segment를 가지게 된다. 이 때, append로 넣어준 웨이 포인트는 4개였는데, Interpolate를 사용하면 이 점들이 좀 더 부드럽게 이어질 줄 알았지만 이 object는 linear한 path segment를 만들어주기 때문에 아무리 250개로 쪼개도 저렇게 4개의 waypoint때와 동일하게 부드럽지 않은 형태로 표현된다. 저걸 만약 부드럽게 표현하시고 싶다면 path를 부드럽게 연결하는 trajectory generation 함수들을 사용할 수 있다. 그리고 난 다음에는 path length라는 메소드로 만들어진 전체 path의 길이를 확인할 수도 있다.
dubinsConnection & dubinsPathSegment object
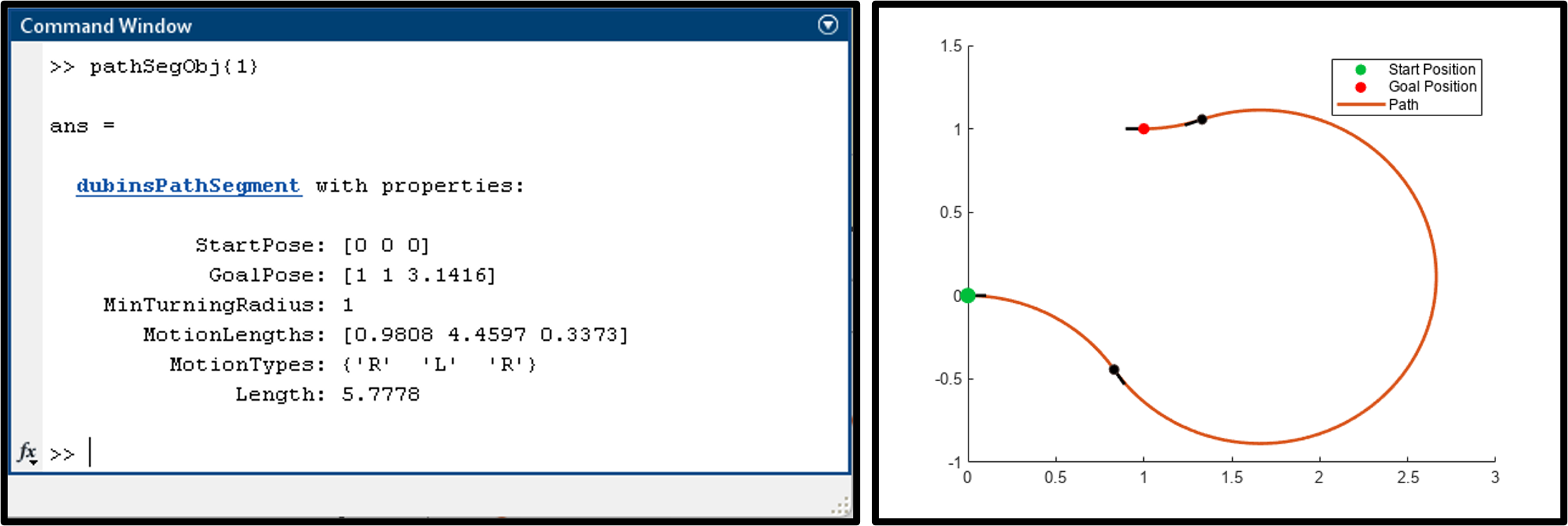
그림 10. dubinsConnection을 이용해 Path를 연결한 결과물 (소스 코드 링크)
두 번째는 Dubins Path이다. Dubins Path는 두 개의 오브젝트가 있는데 dubinsConnection은 두 개의 포즈를 Dubins model로 연결을 하기 위해 필요한 정보를 입력하고 실제로 연결을 해주는 오브젝트이다. 그리고 여기에서 만들어진 결과물을 저장하는 게 dubinsPathSegment 오브젝트이다.
% Create a dubinsConnection object.
dubConnObj = dubinsConnection;
% Define start and goal poses as [x y theta] vectors.
startPose = [0 0 0]; goalPose = [1 1 pi];
% Calculate a valid path segment to connect the poses.
[pathSegObj, pathCosts] = connect(dubConnObj,startPose,goalPose);
% Show the generated path.
show(pathSegObj{1})
코드를 보면 Dubins 커넥션이라고 먼저 오브젝트를 만든다. 여기다가 시작 포즈와 종료 포즈 집어넣고 connect라는 메소드를 이용하면 path segment가 출력되는데 이게 바로 dubinsPathSegment 형태로 되어 있다.
만들어진 dubinsPathSegment 오브젝트를 MATLAB command window에서 쳐보니까 그림 10에서 볼 수 있는 것과 같이 Start Pose는 이렇고 Goal Pose는 이렇고 Min turning radius는 1인데 RLR 타입으로 연결되었으며, 전체길이는 5.778 같은 이런 내용이 있다. navPath와 마찬가지로 interpolate method를 가지고 있고,Show method를 이용해 그려볼수도 있다.
dubinsConnection
| methods | |
|---|---|
| Connect poses for given connection type |
dubinsPathSegment
| methods | |
|---|---|
| Interpolate poses along path segment | |
| Visualize path segment |
reedsSheppConnection & reedsSheppPathSegmentPath object
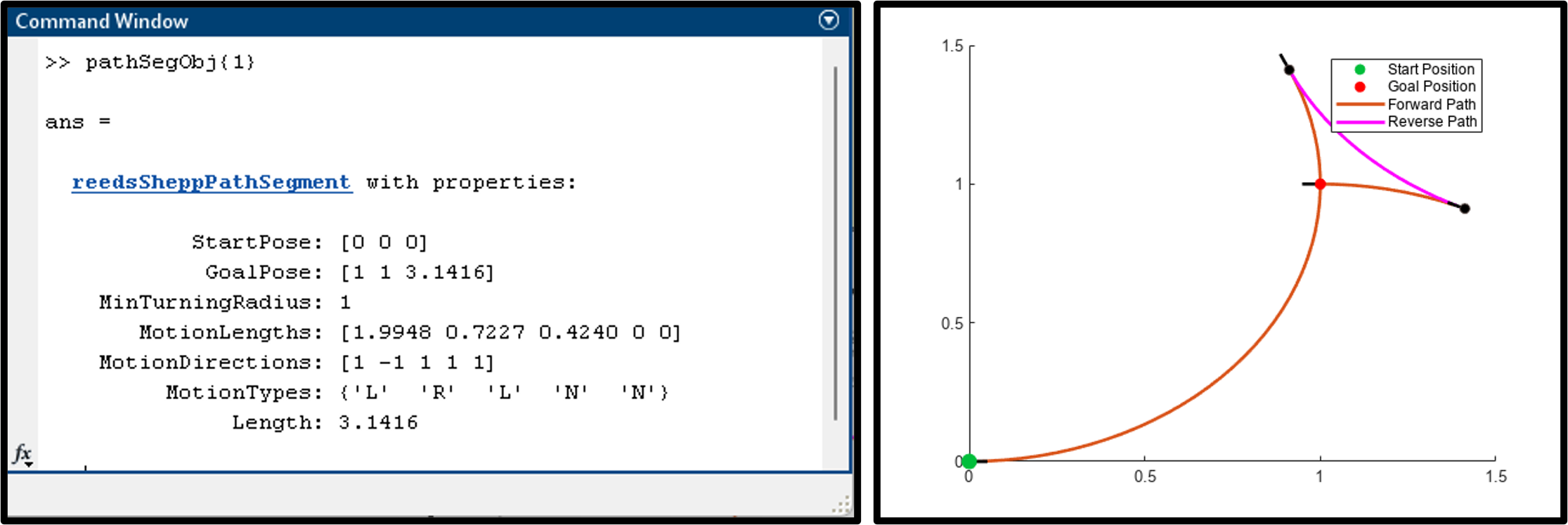
그림 11. reedsSheppConnection을 이용해 Path를 연결한 결과물 (소스 코드 링크)
세 번째로 Reeds-Shepp Path이다. 마찬가지로 reedsSheppConnection과 reedsSheppPathSegmentPath라는 세그먼트 패스라는 오브젝트를 가지고 있다. reedsSheppConnection 오브젝트를 생성해서 똑같이 connect라는 메소드를 이용해서 패스를 만들어보면 이번에는 LRLNN 타입으로 연결이 됐다라고 얘기하는 것을 알 수 있다. 그리고 똑같이 또 그림을 그려줄 수 있다. 초록색 시작 포인트에서 빨간색의 저런 포즈로 가기 위해 두 개의 검은 색 점에서 주행 방향을 바꿔서 목표 지점에 도달한 것을 알 수 있다.
% Create a reedsSheppConnection object.
reedsConnObj = reedsSheppConnection;
% Define start and goal poses as [x y theta] vectors.
startPose = [0 0 0]; goalPose = [1 1 pi];
% Calculate a valid path segment to connect the poses.
[pathSegObj,pathCosts] = connect(reedsConnObj,startPose,goalPose);
% Show the generated path.
show(pathSegObj{1});
reedsSheppConnection
| methods | |
|---|---|
| Connect poses for given connection type |
reedsSheppPathSegment
| methods | |
|---|---|
| Interpolate poses along path segment | |
| Visualize path segment |
Aerial Vehicle Motion Primitives in UAV Toolbox
지금까지의 내용은 Navigation Toolbox에서 지원하는 내용이었다. UAV Toolbox에서도 aerial vehicle 모션 프리미티브를 제공하는데 UAV와 지금까지 언급한 그라운드 모바일 로봇의 차이는 결국은 차원의 문제이다.
uavDubinsConnection & uavDubinsPathSegment object
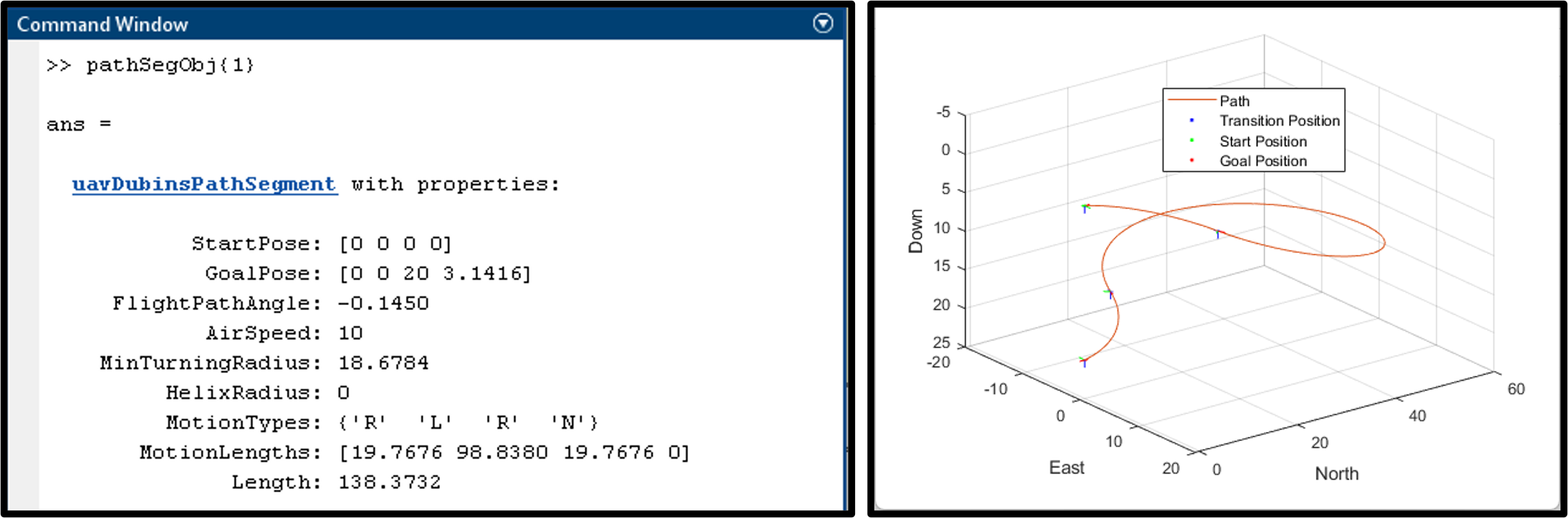
그림 12. uavDubinsConnection을 이용해 UAV용 Path를 연결한 결과물 (소스 코드 링크)
그라운드 모바일 로봇에서는 2차원으로 더빈 커넥션이나 reed shepp 커넥션은 2차원 공간 상에서 연결성을 표현을 해주는데 UAV toolbox에서 제공하는 더빈 커넥션 같은 경우에는 3차원 연결을 해준다. 그렇게 하면 두 pose를 연결하면 이런 식으로 connection이 돼서 3차원 공간상에서 실제로 만들어진 motion 세그먼트가 그림 11에서와 같이 표현되게 된다.
% Create a reedsSheppConnection object.
connectionObj = uavDubinsConnection;
% Define start and goal poses as [x y z theta] vectors.
startPose = [0 0 0 0]; goalPose = [0 0 20 pi];
% Calculate a valid path segment to connect the poses.
[pathSegObj,pathCosts] = connect(connectionObj,startPose,goalPose);
% Show the generated path.
show(pathSegObj{1});
uavDubinsConnection
| methods | |
|---|---|
| Connect poses for given connection type |
uavDubinsPathSegment
| methods | |
|---|---|
| Interpolate poses along path segment | |
| Visualize path segment |
Technical Resources
Path Planning 분야 외의 로봇 개발을 위한 다른 내용이 궁금하다면 아래의 매스웍스 코리아에서 제공하는 모바일 로봇틱스 그리고 자율주행 웹 포털을 통해 정보를 얻어갈 수 있으니 참고하기 바란다.
MATLAB Mobile Robotics Web Portal

그림 12. MATLAB을 이용한 육상 이동 로봇 개발 Web Portal (링크)
MATLAB ADAS Web Portal

그림 13. MATLAB을 이용한 자율주행/ADAS 개발 Web Portal (링크)
MATLAB Onramp Series
매트랩 기초 사용법을 학습하고 싶은 경우 MathWorks 홈페이지 내의 Onramp 라는 무료 트레이닝 코스를 활용할 수 있다. Onramp는 웹상으로 진행하는 온라인 무료 교육으로, 컴퓨터에 매트랩을 설치 할 필요 없이 온라인으로 매트랩 관련된 여러 기초 내용을 학습할 수 있다.
그림 14. MATLAB을 무료로 배울 수 있는 Onramp 시리즈 (링크)